ИЗОБРАЖЕНИЙ МЕТОД

Значение ИЗОБРАЖЕНИЙ МЕТОД в математической энциклопедии:

, отображений метод,- метод теории потенциала для решения некоторых краевых (граничных) задач для дифференциальных уравнений с частными производными в области D, при к-ром выполнение краевых (граничных) условий на границе дD=T достигается путем соответствующего подбора нек-рых дополнительных источников поля, расположенных вне Dи называемых источниками-изображениями.

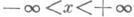Наибольшее развитие И. м. получил в электростатике. Пусть, напр., требуется решить Дирихле задачу для Пуассона уравнения Du=-2pr( х, у )в полуплоскости D={(x, у): y>0, } с заданной на границе Г= {( х, у): y=0, 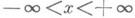} функцией y(x), т. е. требуется найти потенциал электрич. зарядов плотности r( х, у), расположенных в D, при условии, что на Г поддерживается потенциал y(x). Известно, что для решения этой задачи достаточно знать Грина функцию G(x, у; х ₀, y₀), представляющую собой потенциал единичного точечного заряда в точке 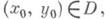когда граница Г заземлена, т. е. G(x,0; х ₀, у ₀)=0- При этом решение и( х, у )исходной задачи выражается через G(x, у; х ₀, у ₀). следующим образом: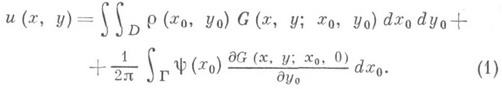

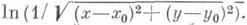Потенциал точечного заряда при отсутствии границ записывается в виде фундаментального решения Лапласа уравнения Добавляя отрицательный единичный заряд-изображение в точке ( х ₀,- у ₀ )и составляя сумму потенциалов этих двух зарядов, получают искомую функцию Грина: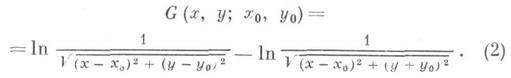

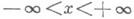В случае полосы D= {(x, у):0<у<b,}, отражая единичный заряд ( х ₀, y₀ )О D от прямых у=0 и у=b, получают бесконечную последовательность зарядов-изображений -1, -1, +1, +1, ..., расположенных, соответственно, в точках ( х ₀,- у ₀),( х ₀,2b- у ₀), ( х ₀, -2b+у ₀),( х ₀, 2b+у ₀),... . Функция Грина в этом случае будет выражаться в виде бесконечного ряда потенциалов точечных зарядов. Для области Dв виде круга D={(r, j):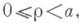

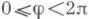} изображением единичного заряда в точке (r₀> j₀) будет отрицательный единичный заряд, расположенный в точке (а ²/r₀, j₀), являющейся отображением точки (r₀, j₀) при помощи инверсии относительно окружности р=а.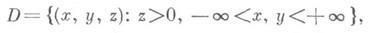

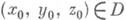Возможны и другие конфигурации границ, составленных из прямых и окружностей, когда решение достигается построением соответствующей последовательности зарядов-изображений.

При решении задачи Дирихле для уравнения Пуассона Du=-4pr(x, у, z )в полупространстве

отражая единичный заряд от плоскости z=0, вместо (2) получают формулу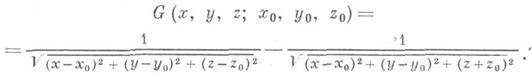

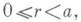
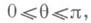
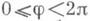В случае шара D={(r,q, j):

} следует применить Кельвина преобразование, и изображением единичного заряда в точке (r₀,q₀, j₀) 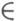Dбудет заряд величины - а/r₀, расположенный в точке (a²/r₀,q₀, j₀), являющейся отображением точки (r₀,q₀, j₀) при помощи инверсии относительно сферы т=а. Отсюда получается, что если известно решение уравнения Пуассона Du=-4pr(r, q, j) в нек-рой области D, то функция v(r,q, j)=(а/r)u(а ²/r, q, j) дает решение уравнения Пуассона Dv=-4pr'(r, q, j) с плотностью r' (r, q, j)=(а/r)⁵r(а ²/r, q, j) в области D', являющейся отображением Dпри инверсии относительно сферы r=а. В такой форме И. м. иногда наз. методом инверсии. При применении метода инверсии необходимо обращать внимание на то, что краевые (граничные) условия, вообще говоря, также преобразуются.

Для более сложных пространственных областей, граница к-рых состоит из нескольких плоскостей или сфер, возможно также применение бесконечных последовательностей зарядов-изображений. В комбинации с предельными переходами, когда один или несколько источников удаляются в бесконечность, И. м. допускает решение и более сложных задач таких, напр., как отыскание потенциала электростатич. поля в случае проводящего шара, помещенного в однородном на бесконечности поле.

В случае уравнения Гельмгольца Du+k²u=0 И. м. применим только для областей, ограниченных прямыми, или для пространственных областей, ограниченных плоскостями, с использованием соответствующих фундаментальных решений H⁽¹⁾₀(kr), H⁽²⁾₀(kr) или e^ikr/r,e^-ikr/r.

Лит.:[1] Гринберг Г. А., Избр. вопросы математической теории электрических и магнитных явлений, М.- Л., 1948; [2] Смайт В., Электростатика и электродинамика, пер. с англ., М., 1954; [3] Кочин Н. Е., Кибель И. А., Розе Н. В., Теоретическая гидромеханика, т. 1, М.- Л., 1963.

Е. Д. Соломенцев.