"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ИЗМЕРИМОЕ ОТОБРАЖЕНИЕ
Значение ИЗМЕРИМОЕ ОТОБРАЖЕНИЕ в математической энциклопедии:
- отображение f измеримого пространства  в измеримое пространство
в измеримое пространство 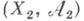 такое, что
такое, что

В случае, когда  есть а-алгебра, а
есть а-алгебра, а  - действительная прямая с s-алгеброй А 2 борелевских множеств, понятие И. о. сводится к понятию измеримой функции (однако, когда
- действительная прямая с s-алгеброй А 2 борелевских множеств, понятие И. о. сводится к понятию измеримой функции (однако, когда 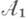 есть лишь s-кольцо, определение измеримой функции обычно видоизменяется в связи с нуждами теории интегрирования). Суперпозиция И. о. измерима. Если
есть лишь s-кольцо, определение измеримой функции обычно видоизменяется в связи с нуждами теории интегрирования). Суперпозиция И. о. измерима. Если 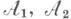 - кольца, и
- кольца, и 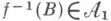 для любого Виз нек-рого класса множеств
для любого Виз нек-рого класса множеств 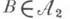 такого, что кольцо, им порожденное, совпадает с
такого, что кольцо, им порожденное, совпадает с 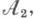 то f измеримо. Аналогичное утверждение верно и для случая s-колец, алгебр и s-алгебр. Если
то f измеримо. Аналогичное утверждение верно и для случая s-колец, алгебр и s-алгебр. Если  - топологич. пространства са-алгебрами борелевских множеств, то всякое непрерывное отображение Х 1 в Х 2 измеримо. Пусть X - топологич. пространство,
- топологич. пространства са-алгебрами борелевских множеств, то всякое непрерывное отображение Х 1 в Х 2 измеримо. Пусть X - топологич. пространство,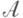 есть а-алгебра его борелевских подмножеств и m -конечная неотрицательная регулярная мера на
есть а-алгебра его борелевских подмножеств и m -конечная неотрицательная регулярная мера на 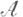 (регулярность означает, что m(A)=sup {m(F) :
(регулярность означает, что m(A)=sup {m(F) : Fзамкнуто}). Пусть, далее, S- сепарабельное метрич. пространство,
Fзамкнуто}). Пусть, далее, S- сепарабельное метрич. пространство,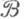 есть а-алгебра его борелевских подмножеств и f- измеримое отображение
есть а-алгебра его борелевских подмножеств и f- измеримое отображение  и
и 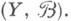 Тогда для любого e>0 найдется замкнутое подмножество
Тогда для любого e>0 найдется замкнутое подмножество  такое, что
такое, что 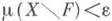 и f непрерывно sa F (теорема Лузина).
и f непрерывно sa F (теорема Лузина).
Лит..: [1] Xалмош П., Теория меры, пер. с англ., М.,. 1953; [2] Невё Ж., Математические основы теории вероятностей, пер. с франц., М., 1969; [3] Бурбаки Н., Интегрирование. Меры, интегрирование мер, пер. с франц., М., 1967; [4] Данфорд Н., Шварц Дж., Линейные операторы. Общая теория, пер. с англ., М., 1962.
В. В. Сазонов.

 в измеримое пространство
в измеримое пространство 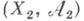 такое, что
такое, что
 есть а-алгебра, а
есть а-алгебра, а  - действительная прямая с s-алгеброй А 2 борелевских множеств, понятие И. о. сводится к понятию измеримой функции (однако, когда
- действительная прямая с s-алгеброй А 2 борелевских множеств, понятие И. о. сводится к понятию измеримой функции (однако, когда 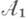 есть лишь s-кольцо, определение измеримой функции обычно видоизменяется в связи с нуждами теории интегрирования). Суперпозиция И. о. измерима. Если
есть лишь s-кольцо, определение измеримой функции обычно видоизменяется в связи с нуждами теории интегрирования). Суперпозиция И. о. измерима. Если 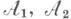 - кольца, и
- кольца, и 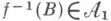 для любого Виз нек-рого класса множеств
для любого Виз нек-рого класса множеств 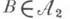 такого, что кольцо, им порожденное, совпадает с
такого, что кольцо, им порожденное, совпадает с 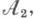 то f измеримо. Аналогичное утверждение верно и для случая s-колец, алгебр и s-алгебр. Если
то f измеримо. Аналогичное утверждение верно и для случая s-колец, алгебр и s-алгебр. Если  - топологич. пространства са-алгебрами борелевских множеств, то всякое непрерывное отображение Х 1 в Х 2 измеримо. Пусть X - топологич. пространство,
- топологич. пространства са-алгебрами борелевских множеств, то всякое непрерывное отображение Х 1 в Х 2 измеримо. Пусть X - топологич. пространство,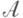 есть а-алгебра его борелевских подмножеств и m -конечная неотрицательная регулярная мера на
есть а-алгебра его борелевских подмножеств и m -конечная неотрицательная регулярная мера на 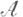 (регулярность означает, что m(A)=sup {m(F) :
(регулярность означает, что m(A)=sup {m(F) : Fзамкнуто}). Пусть, далее, S- сепарабельное метрич. пространство,
Fзамкнуто}). Пусть, далее, S- сепарабельное метрич. пространство,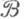 есть а-алгебра его борелевских подмножеств и f- измеримое отображение
есть а-алгебра его борелевских подмножеств и f- измеримое отображение  и
и 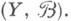 Тогда для любого e>0 найдется замкнутое подмножество
Тогда для любого e>0 найдется замкнутое подмножество  такое, что
такое, что 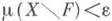 и f непрерывно sa F (теорема Лузина).
и f непрерывно sa F (теорема Лузина).