"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
АБЕЛЯ-ПУАССОНА МЕТОД СУММИРОВАНИЯЗначение АБЕЛЯ-ПУАССОНА МЕТОД СУММИРОВАНИЯ в математической энциклопедии:
один из методов суммирования рядов Фурье. Ряд Фурье функции  суммируется методом Абеля - Пуассона в точке j к числу 5, если суммируется методом Абеля - Пуассона в точке j к числу 5, если
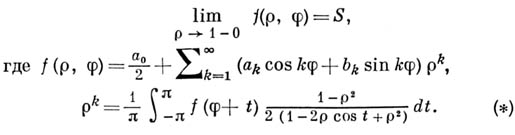
Если  то интеграл в правой части есть гармонич. функция для то интеграл в правой части есть гармонич. функция для  и, как показал С. Пуассон (S. Poisson), является решением задачи Дирихле для круга. В связи с этим Абеля метод суммирования в применении к рядам Фурье наз. А.- П. м. с., а интеграл и, как показал С. Пуассон (S. Poisson), является решением задачи Дирихле для круга. В связи с этим Абеля метод суммирования в применении к рядам Фурье наз. А.- П. м. с., а интеграл  - Пуассона интегралом. - Пуассона интегралом.
Если  - полярные координаты точки внутри круга радиуса 1, то можно рассматривать предел функции - полярные координаты точки внутри круга радиуса 1, то можно рассматривать предел функции  когда точка когда точка  стремится к точке на окружности не по радиальному, но и не по касательному и даже произвольному пути. Так, имеет место теорема Фату: если функция стремится к точке на окружности не по радиальному, но и не по касательному и даже произвольному пути. Так, имеет место теорема Фату: если функция  принадлежит принадлежит  и непрерывна в точке и непрерывна в точке  то то
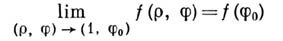
независимо от способа стремления точки  к точке к точке  при условии, что она остается внутри круга радиуса 1. при условии, что она остается внутри круга радиуса 1.
Лит.:[1] Бари Н. К., Тригонометрические ряды, М., 1961. А. А. Захаров.
|

 суммируется методом Абеля - Пуассона в точке j к числу 5, если
суммируется методом Абеля - Пуассона в точке j к числу 5, если 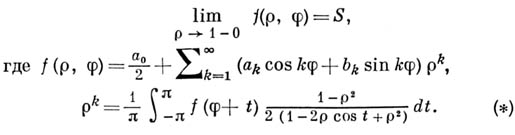
 то интеграл в правой части есть гармонич. функция для
то интеграл в правой части есть гармонич. функция для  и, как показал С. Пуассон (S. Poisson), является решением задачи Дирихле для круга. В связи с этим Абеля метод суммирования в применении к рядам Фурье наз. А.- П. м. с., а интеграл
и, как показал С. Пуассон (S. Poisson), является решением задачи Дирихле для круга. В связи с этим Абеля метод суммирования в применении к рядам Фурье наз. А.- П. м. с., а интеграл  - Пуассона интегралом.
- Пуассона интегралом. - полярные координаты точки внутри круга радиуса 1, то можно рассматривать предел функции
- полярные координаты точки внутри круга радиуса 1, то можно рассматривать предел функции  когда точка
когда точка  стремится к точке на окружности не по радиальному, но и не по касательному и даже произвольному пути. Так, имеет место теорема Фату: если функция
стремится к точке на окружности не по радиальному, но и не по касательному и даже произвольному пути. Так, имеет место теорема Фату: если функция  принадлежит
принадлежит  и непрерывна в точке
и непрерывна в точке  то
то 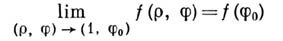
 к точке
к точке  при условии, что она остается внутри круга радиуса 1.
при условии, что она остается внутри круга радиуса 1.