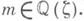ИДЕАЛЬНОЕ ЧИСЛО

Значение ИДЕАЛЬНОЕ ЧИСЛО в математической энциклопедии:

- элемент полугруппы D дивизоров кольца Ацелых чисел нек-рого поля алгебраич. чисел. Полугруппа D- коммутативная свободная полугруппа с единицей; ее свободные образующие наз. простыми идеальными числами. В современной терминологии И. ч. наз. целыми дивизорами кольца А. Они допускают естественное отождествление с идеалами кольца А.

И. ч. были введены в связи с отсутствием однозначности разложения на простые множители в кольцах целых алгебраич. чисел. Для каждого разложение соответствующего дивизора j(а). в произведение простых И. ч. можно рассматривать как нек-рую замену однозначности разложения на простые множители в случае, когда такое разложение в кольце А неоднозначно.

Напр., кольцо Авсех целых чисел поля состоит из всех чисел вида а+bс целыми аи b. В этом кольце число 6 допускает два различных разложения на множители:

причем числа 2, 3, и - простые попарно неассоциированные элементы кольца А; таким образом, разложение на простые множители в Анеоднозначно. Однако в полугруппе Dэлементы j(2), j(3), j(1+), ф(1-) не будут простыми, а именно:

где - простые И. ч. в

D. Таким образом, два разложения числа 6 на простые множители в кольце Апродолжаются до одного и того же разложения в D.

Понятие И. ч. было введено Э. Куммером (Е. Rummer) в связи с исследованием арифметики круговых полей (см. [1] - [2]). Пусть K=Q(z) - поле деления круга на р частей и А= Z(x) - кольцо целых чисел поля AT. И. ч. для кольца A определялись как произведение простых И. ч., а эти последние - как "идеальные" простые делители простых натуральных чисел. Для построения всех простых И. ч., делящих заданное простое натуральное q, использовалась Куммера теорема. Пользуясь тем, что Аимеет степенной базис 1, x, x², . . .,x^p-2 над Z, Э. Куммер рассматривал разложение кругового многочлена F_р (Х). в кольце Z/qZ[X]. И. ч., делящими число q, объявлялись элементы, находящиеся во взаимно однозначном соответствии с неприводимыми множителями F_р (Х)в Z/qZ[X](несколько другого подхода требовал случай p = q). Специальный метод применялся для определения показателя степени, с к-рым данное простое И. ч. входит в данное Аналогичный метод он разработал для создания теории делимости в полях вида Q(x,), где

Перенесение теории И. ч. на случай произвольного поля алгебраических чисел принадлежит в основном Л. Кронекеру (L. Kronecker) и Р. Дедекинду (R. Dedekind). Уже в их работах наметилось разделение теории И. ч. на теорию дивизоров (подход Л. Кронекера) и теорию идеалов. Р. Дедекинд каждому И. ч. взаимно однозначно сопоставлял идеал кольца А, к-рый определялся им как подмножество в А, состоящее из О и всех таких а, что аделится на это И. ч. При этом, если а ₁,. . ., а _п- образующие, идеала I, то соответствующее I И. ч. является наибольшим общим делителем И. ч. j(a₁), . . ., j(a_n).

Впоследствии понятие идеала было распространено на случай произвольного кольца А; кольца, для к-рых понятия идеала и дивизора совпадают, наз. теперь дедекиндовыми.

Лит.:[1] Kummer E., "J. reine und angew. Math.", 1847, Bd 35, S. 319-26, 327-67; [2] его же, "J. math, pure.s etappl.", 1851, t. 16, p. 377-498; [3] Edward HaroldM., "Arch. Hist. Exact. Sci.", 1975, v. 14, № 3, p. 219-36; L4] Бурбаки H., Коммутативная алгебра, пер. с франц., М., 1971; [5] его же, Очерки по истории математики, пер. с франц., М., 1963.

Л. В. Кузьмин.