|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ИГРА С ИЕРАРХИЧЕСКОЙ СТРУКТУРОЙЗначение ИГРА С ИЕРАРХИЧЕСКОЙ СТРУКТУРОЙ в математической энциклопедии: - модель конфликтной ситуации при фиксированной последовательности ходов и обмена информацией участников. Основным объектом исследования в теории И. с и. с. является задача об отыскании наибольшего гарантированного результата и оптимальной стратегии выделенного игрока. Пусть игроки I, II стремятся к увеличению, соответственно, функций выигрыша f1(x1 , х 2 )и f2(x1, х 2), непрерывных на произведении компактов Х 1, Х 2; Игра Г 1. Игрок I выбирает
- множество оптимальных выборов игрока II. Тогда наибольший гарантированный результат игрока I равен
Игра Г 2. Игрок I рассчитывает иметь и действительно будет иметь информацию о выборах игрока II; сообщает свою стратегию - функцию
где множество оптимальных выборов игрока II есть
Игра Г 3. Игрок I рассчитывает иметь и действительно будет иметь информацию о выборах игрока II вида
где
Соотношение между результатами в этих играх определяет для игрока I значимость информации о действиях игрока II: Развиты методы решения игры Г 1; использующие штрафные функции, необходимые условия оптимальности, приближение исходной игры игрой с однозначными ответами игрока II. Полностью решены частные классы игр: с близкими интересами, биматричные, билинейные и др. Задача отыскания G1 некорректна относительно изменения функции f2(x1, х 2 )в равномерной метрике и множеств Х 1, Х 2 в метрике Хаусдорфа. Предложен общий метод регуляризации решения игры Г 1; регуляризация задачи по функции выигрыша игрока II осуществляется за счет введения искусственной неточности определения. Отыскание величины G2 сводится к решению Пусть для любого е>0 определены функции, множества и величины:
В указанных условиях G2=max[K, M]и стратегия
гарантирует игроку I при достаточно малых е получение тaх[ К, M]-e. Как видно из определения, оптимальная стратегия состоит из нескольких ветвей, последняя играет роль стратегии наказания. Если L2<f2(x1, x2 )и у функции f2(x1, х 2 )нет локальных максимумов со значением L2 на Х 1 Аналогичным образом может быть найдено решение игры Г 3, оно также сводится к решению ряда задач математич. программирования. При введении в И. с и. с. побочных платежей со стороны игрока I, как функций от выборов игрока II, выражение для наибольшего гарантированного результата игрока I значительно упрощается. В игре Г 2, где
Вообще применение сколь угодно малых побочных платежей z(x2 )в И. с и. с. позволяет игроку I реализовать наибольший гарантированный результат, рассчитанный на благожелательность партнера. Сформулированные игры допускают обобщение на случай постепенного получения и использования информации в динамике. В случае, когда состояние игроков описывается дифференциальными или разностными уравнениями, возникает обширный класс задач, связанный с разнообразием форм информированности игроков о состоянии и течении как физич. процесса, так и процесса принятия решения. Рассмотрены обобщения игр Т 1 и Г 2 на случай запрещенных ситуаций, т. е. при наличии совместных ограничений на выборы игроков. Приведенные формулировки относятся к случаю полной информированности игрока I о функции выигрыша и множестве его выборов. Если игроку I известно, что непрерывная функция выигрыша игрока II удовлетворяет неравенствам
при известных непрерывных функциях f-2( х 1, х 2), f+2(x1, х 2), то его наибольший гарантированный результат в игре Г 2 определяется из условия максимизации функции от одной переменной. Более общий вариант неполной информированности игрока I об интересах игрока II состоит в следующем: игроку I известна функция f2(x1, x2, а), Близка к рассмотренным задача об отыскании наибольшего гарантированного результата игрока I в игре Г 2 при наличии в функциях выигрышей игроков параметра а, характеризующего природную неопределенность, когда игрок II при своем выборе информирован о конкретной величине а, а игрок I не информирован. В случае, когда игра Г 2 при неопределенности повторяется, информированность игрока I об интересах и возможностях игрока II может быть повышена за счет информации, содержащейся в откликах игрока II на действия игрока I. Построены соответствующие процедуры, позволяющие игроку I, начиная с нек-рой партии, получать результат, сколь угодно близкий к результату, гарантированному ему при полной информированности. Такие же результаты получены и в игре Г 1 с неопределенностями. Если моменты получения игроком I информации о неопределенном факторе а не фиксированы, то игрок I может получить в остальных повторениях результат, сколь угодно близкий к гарантированному ему в условиях полной информированности, при более слабых предположениях относительно функций выигрышей участников. Кроме того, в игре Г 1 аналогичный результат игрок I может получить, наблюдая только за значениями собственной функции выигрыша. Формулировки рассматриваемых игр естественно переносятся на случай многих лиц, взаимодействия к-рых в смысле приоритета действий и передачи информации имеют иерархическую структуру. При анализе этих игр необходимо оговаривать также правила взаимодействий игроков одного уровня. Так, при рассмотрении игры трех лиц, где функции выигрышей игроков имеют вид
х 1 О Х 1, х 2 О Х 2, х 3 О Х 3, для отыскания наибольшего гарантированного результата выделенного игрока I, обладающего приоритетом в действиях, необходимо конкретизировать его информацию о поведении игроков II и III. Если игроки II и III образуют известную игроку I жесткую коалицию, т. е. формулируют коалиционный критерий и сообща определяют свои выборы, то для игрока I данный случай эквивалентен рассмотренным ранее играм двух лиц. Обозримые результаты получаются также в случае, когда игроки II и III либо находятся в известной игроку I коалиции, либо действуют индивидуально, если таким образом могут получить результат больший, чем дает коалиция; при этом каждый из игроков II и III не имеет самостоятельной информации о ходе другого и порядок их ходов задается игроком I. Подробно проанализированы игры, имеющие "веерную" структуру: выделенный игрок (управляющий центр) П 0 и пигроков на следующем уровне иерархии (производители продукции) стремятся к увеличению функций выигрыша f0(x0, х)и fi(xi0; х i),i=l, ..., п, соответственно, где х 0= {х i0, ..., х n0)- выбор П 0, При помощи И. с и. с. получают естественную интерпретацию различные механизмы централизованного управления активными экономич. подсистемами. Игра Г 1 описывает процесс централизованного управления при помощи цен; игра Г 2 моделирует политику штрафов и поощрений при стимулировании производства; игрой Г 3 моделируется процесс распределения ресурсов как функций от производственных способов использования данных ресурсов. Лит.:[1] Гермейер Ю. Б., Игры с непротивоположными интересами, М., 1972. И. А. Вателъ, Ф. II. Ерешко. |
|
|
|

 . В зависимости от характера информации и порядка ходов могут быть сформулированы следующие различные игры.
. В зависимости от характера информации и порядка ходов могут быть сформулированы следующие различные игры. и сообщает свой выбор игроку II. Пусть
и сообщает свой выбор игроку II. Пусть

 где
где - множество всех отображений из Х 2 в X1 игроку II. Наибольший гарантированный результат игрока I равен
- множество всех отображений из Х 2 в X1 игроку II. Наибольший гарантированный результат игрока I равен
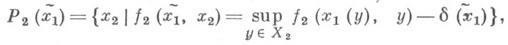
 при этом
при этом  тогда и только тогда, когда достигается max f2(x1(y), у).
тогда и только тогда, когда достигается max f2(x1(y), у). где
где  - множество всех отображений из X1 в Х 2;сообщает игроку II свою стратегию
- множество всех отображений из X1 в Х 2;сообщает игроку II свою стратегию  где
где  - множество всех отображений из
- множество всех отображений из  в Х 1. Наибольший гарантированный результат игрока I равен
в Х 1. Наибольший гарантированный результат игрока I равен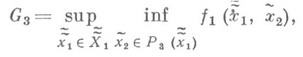

 при этом
при этом  тогда и только тогда, когда достигается
тогда и только тогда, когда достигается 
 Пользуясь указанной схемой в построении стратегий игроков, можно формулировать игры с произвольной глубиной рекурсии. Имеет место утверждение: в играх Г 2m, m>1, наибольший гарантированный результат игрока I равен G2; в играх Г 2m+1, m>1, наибольший гарантированный результат равен G3. Задача отыскания G1 относится к классу задач на максимин со связанными ограничениями.
Пользуясь указанной схемой в построении стратегий игроков, можно формулировать игры с произвольной глубиной рекурсии. Имеет место утверждение: в играх Г 2m, m>1, наибольший гарантированный результат игрока I равен G2; в играх Г 2m+1, m>1, наибольший гарантированный результат равен G3. Задача отыскания G1 относится к классу задач на максимин со связанными ограничениями. ряда задач математического программирования.
ряда задач математического программирования.

 Х 2, то
Х 2, то  и оптимальная стратегия имеет простой вид:
и оптимальная стратегия имеет простой вид: 

 и игрок I выбирает стратегии х 1( х 2), z(x2), отыскание G2 сводится к решению задачи математич. программирования
и игрок I выбирает стратегии х 1( х 2), z(x2), отыскание G2 сводится к решению задачи математич. программирования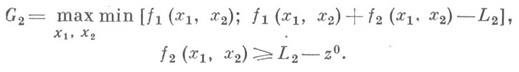

 . и известно, что при нек-ром (неизвестном) значении a=a0 истинная функция f2(x1, x2)=f2(x1, х 2,a0). При такой информированности решение игры Г 2 для конечных множеств Асводится к максимизации функции нескольких переменных; при бесконечных множествах Азадача еще более сложна. Наличие неопределенных факторов в постановке игры Г 1 не приводит к принципиальному усложнению задачи, поскольку этот случай сводится к игре без неопределенностей. Для игры Г 2 при неопределенности рассмотрен ряд задач, когда понятие стратегии игроков расширено за счет предложения игрока I игроку II сообщить свой критерий эффективности, т. е. нек-рое
. и известно, что при нек-ром (неизвестном) значении a=a0 истинная функция f2(x1, x2)=f2(x1, х 2,a0). При такой информированности решение игры Г 2 для конечных множеств Асводится к максимизации функции нескольких переменных; при бесконечных множествах Азадача еще более сложна. Наличие неопределенных факторов в постановке игры Г 1 не приводит к принципиальному усложнению задачи, поскольку этот случай сводится к игре без неопределенностей. Для игры Г 2 при неопределенности рассмотрен ряд задач, когда понятие стратегии игроков расширено за счет предложения игрока I игроку II сообщить свой критерий эффективности, т. е. нек-рое  так чтобы окончательный выбор х 1 мог быть сделан по получении информации о х 2 и критерия эффективности игрока II. Если в этом случае игрок II осторожен, т. е. придерживается принципа наибольшего гарантированного результата, а игрок I сообщает ему параметризованную стратегию
так чтобы окончательный выбор х 1 мог быть сделан по получении информации о х 2 и критерия эффективности игрока II. Если в этом случае игрок II осторожен, т. е. придерживается принципа наибольшего гарантированного результата, а игрок I сообщает ему параметризованную стратегию  то можно показать, что наибольший гарантированный результат игрока I равен
то можно показать, что наибольший гарантированный результат игрока I равен  где G2a - наибольший гарантированный результат игрока I в игре Г 2 при данном
где G2a - наибольший гарантированный результат игрока I в игре Г 2 при данном  Аналогичный результат без предположения об осторожности игрока II имеет место, когда игроку I известно параметрич. семейство множеств Х 2(a),
Аналогичный результат без предположения об осторожности игрока II имеет место, когда игроку I известно параметрич. семейство множеств Х 2(a), одно из к-рых совпадает с истинным.
одно из к-рых совпадает с истинным.
 х- {х 1, ..., х n}- совокупный выбор игроков на нижнем уровне иерархии, причем они действуют независимо, и каждый игрок номера iраспоряжается выбором х i О Х i. Все множества полагаются компактными, а функции непрерывными. Игрок П 0 рассчитывает на информацию (и будет ее иметь) о выборах
х- {х 1, ..., х n}- совокупный выбор игроков на нижнем уровне иерархии, причем они действуют независимо, и каждый игрок номера iраспоряжается выбором х i О Х i. Все множества полагаются компактными, а функции непрерывными. Игрок П 0 рассчитывает на информацию (и будет ее иметь) о выборах 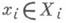 и сообщает каждому игроку i соответствующую стратегию функцию
и сообщает каждому игроку i соответствующую стратегию функцию  определенную на Xi со значениями из Х i0. Для И. с и. с. плиц получены выражения наибольшего гарантированного результата выделенного игрока при различных расширениях его класса стратегий за счет передачи игрокам нижнего уровня информации о действиях партнеров, а также введения элементов блефа. Как и в играх двух лиц, возможность побочного платежа со стороны выделенного игрока значительно упрощает отыскание его гарантированного результата.
определенную на Xi со значениями из Х i0. Для И. с и. с. плиц получены выражения наибольшего гарантированного результата выделенного игрока при различных расширениях его класса стратегий за счет передачи игрокам нижнего уровня информации о действиях партнеров, а также введения элементов блефа. Как и в играх двух лиц, возможность побочного платежа со стороны выделенного игрока значительно упрощает отыскание его гарантированного результата.