|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ИГР ТЕОРИЯЗначение ИГР ТЕОРИЯ в математической энциклопедии: - теория математических моделей принятия оптимальных решений в условиях конфликтов. Формальное определение игры. Под конфликтом понимают явление, применительно к к-рому можно говорить, кто и как в этом явлении участвует, какие у него могут быть исходы и кто и как в этих исходах заинтересован. Поэтому для формального задания конфликта необходимо указать: 1) множество
наз. игрой. Содержание И. т. состоит в установлении связей между компонентами каждой игры и "оптимальными" ее исходами, и прежде всего: в уточнении самого понятия оптимальности, в доказательстве существования оптимальных исходов и в их фактич. определении. Развитие И. т. приводит к вопросам изучения взаимосвязей между различными играми, что выражается в разработке разного рода исчислений игр, и к рассмотрению классов, пространств, категорий игр. Классификация игр. Игры, в к-рых совсем нет коалиций интересов пли же имеется лишь одна такая коалиция, являются предметами изучения чисто дескриптивных или же традиционных оптимизационных теорий. Игры в собственном смысле слова имеют не менее двух коалиций интересов. Обычно в И. т. как коалиции действия, так и коалиции интересов принято атомизировать и считать как те, так и другие подмножествами нек-рого множества I, элементы к-рого наз. игроками. Вначале множество игроков в игре принималось конечным, но позднее (1970-е гг.) начали изучаться игры и с бесконечными и притом неатомическнми множествами игроков. Для игр с одной коалицией действия множество всех ситуаций можно принять за множество стратегий этой единственной коалиции действия и далее о стратегиях не упоминать. Поэтому такие игры наз. нестратегическими. В отличие от них, все остальные игры, с двумя или более коалициями действия, наз. стратегическими. Весьма широкий класс нестратегич. игр может быть получен следующим образом. Пусть I- множество игроков, и
где v(K)- некоторое действительное число, а
то получится классическая кооперативная игра. В этом случае определение v(K)означает возможность коалиции Куверенно добиться суммарного выигрыша v(K)и произвольно перераспределить его между своими членами. Определение Нозначает, что общая распределяемая в игре сумма есть v(I)(распределять меньшую сумму невыгодно; большей же просто нет!), а каждый игрок iбудет соглашаться лишь на долю xi, не меньшую, чем та сумма v(i), к-рую он может уверенно получить самостоятельно. Эсновной класс стратегич. игр составляют бескоалиционные игры, в к-рых множество игроков I совпадает с множествами коалиций действия Таким образом, бескоалиционная игра может быть описана в виде тройки Г= <I, Если все множества стратегий Если I={I, II} и Н I (х)=-HII(x) для всех Если в антагонистич. игре Пусть I - множество игроков,
наз. общей позиционной игрой. В конечном счете в такой игре выигрыш каждого игрока вполне определяется складыварщейся ситуацией, т. е. выбором стратегий всеми игроками. Поэтому такие игры относятся к числу бескоалиционных игр. Пусть в общей позиционной игре Г компонента Xявляется конечномерным евклидовым пространством, Т- множеством действительных чисел, а j:
(равенство понимается как векторное) имеет при данных начальных условиях единственное решение. Тогда каждая ситуация определяет некоторую партию, к-рая в данном случае наз. траекторией. Так определенная игра наз. дифференциальной игрой. К числу общих позиционных игр относятся также позиционные игры и динамические игры (в том числе стохастические игры, рекурсивные игры, а также игры на выживание). Основные результаты теории игр. Основная проблематика в И. т. связана с принципами оптимальности, которые, во-первых, должны в достаточной мере отражать содержательные представления об оптимальности, а во-вторых, должны быть реализуемыми на достаточно широких и естественно очерченных классах игр. Эти два требования, предъявляемые к принципам оптимальности, в известной мере противоречат друг другу, и поэтому для многих содержательно естественных классов игр И. т. еще не выработала соответствующих принципов оптимальности. Вместе с тем известны классы игр, обслуживаемые с равным успехом несколькими различными принципами оптимальности. Поэтому конструирование и анализ принципов оптимальности являются существенной составной частью И. т. Каждый принцип оптимальности реализуется (не обязательно однозначно) в виде множества ситуаций-оптимумов. Это множество (к-рое может оказаться пустым) наз. решением. Логической основой каждого решения являются нек-рые черты обычного экстремума, сформулированные применительно к одновременной экстремизации нескольких функций. Поэтому, помимо стремления к наибольшим (в арифметическом смысле) значениям выигрышей, решения игр могут выражать нек-рые характеристики устойчивости и симметрии, а также различные комбинации того и другого. Так, среди черт оптимальности в нестратегич. играх можно назвать недоминируемость, т. е. соглашение считать оптимальными те и только те ситуации х, для к-рых ни при какой ситуации уи коалиции интересов Кне может быть Формулы и алгоритмы, позволяющие находить решения игр, также можно отнести к числу принципов оптимальности (с узкой областью применимости). Напр., в матричной игре с диагональной матрицей выигрышей принципом оптимальности можно считать выбор игроками стратегий с вероятностями, обратно пропорциональными соответствующим диагональным элементам матрицы. Реализуемость принципа оптимальности для нек-рого класса игр состоит в существовании для всех игр этого класса соответствующих (непустых) множеств оптимумов. Их отсутствие в первоначально заданных ситуациях может преодолеваться путем расширения множеств стратегий (и тем самым - множеств конструируемых из них ситуаций). Для бескоалиционных игр плодотворно используются смешанные (рандомизированные) стратегии. Большинство доказательств теорем существования решений в И. т. носит неэффективный характер (многие из них опираются на теоремы о неподвижной точке) и не содержат алгоритмов нахождения решений. Поэтому в И. т. важны частные аналитические и численные методы нахождения решений. При этом вопрос о фактическом нахождении решений игр нередко оказывается очень сложным, и ответ на него удается найти лишь для весьма узких классов игр. В разработке исчислений игр можно выделить несколько направлений. Изучаются возможности нахождения и описания (хотя бы частичного) решений одной игры на основе решений другой игры, в том или ином смысле более просто устроенной. Элементарными примерами таких редукций могут служить естественное отбрасывание доминируемых стратегий игроков в бескоалиционных играх, симметризация таких игр, а также аппроксимации бесконечных игр конечными. Редукционным процессом можно считать также предложенное Дж. Нейманом (J. Neumann) построение кооперативной модели бескоалиционной игры. Известны и обратные результаты, указывающие на принципиальную несводимость решений игр того или иного класса к решению игр более узкого класса. Напр., можно указать бескоалиционные игры трех лиц, решение к-рых связано с выполнением иррациональных операций, в то время как решение биматричных игр всегда осуществимо при помощи рациональных операций. Фиксация одних компонент в играх нек-рого класса (напр., множества игроков и множеств их стратегий в условиях класса всех бескоалиционных игр) и различение игр по остальным компонентам (в данном примере - по функциям выигрыша игроков) приводит к рассмотрению пространств игр, к-рое осуществляется средствами функционального анализа и топологии. Введение на таких пространствах игр вероятностной меры приводит к стохастич. играм. Связи теории игр с другими разделами математики. И. т. тесно связана с различными разделами математики. Как общая теория множеств с несколькими бинарными отношениями, она близка алгебре. В И. т. используется весьма разнообразный математич. аппарат, а большое число вполне традиционных математич. задач допускает теоретико-игровые обобщения. Оптимальные поведения в стратегич. играх обычно оказываются рандомизированными, поэтому теоретико-вероятностные понятия настолько естественно входят в И. т. и употребляются в ней, что одно время даже было принято считать И. т. частью теории вероятностей. Математич. модели исследования операций (являющиеся моделями принятия оптимальных решений) естественно распределяются по трем уровням: детерминированному, стохастическому и неопределенному - в зависимости от степени информированности принимающих решения субъектов. Принятие решения в условиях неопределенности можно интерпретировать как конфликт принимающего решение субъекта против "природы" и тем самым - как игру. По существу к играм относятся и все многокритериальные задачи. Поэтому И. т. в ее методологич. основах и в практич. ориентированности можно считать разделом исследования операций. И. т. является рдной из составных частей математич. аппарата кибернетики. В динамич. играх стратегии выступают как функции "информационных состояний" игроков, причем в ходе игры игроки могут приобретать или утрачивать информацию. Это обусловливает связь И. т. с информации теорией. Приложения теории игр. Помимо разнообразных связей внутри математики, И. т. имеет многочисленные приложения вне ее. Они касаются главным образом тех отраслей знаний и видов практич. деятельности, к-рые непосредственно имеют дело с конфликтами: военного дела, капиталистич. экономики (в частности, И. т. применяется в вопросах борьбы фирм за рынки, в явлениях олигополии, в планировании рекламных компаний, при формировании цен на конкурентных рынках, в биржевой игре и т. д.), права и т. п. С позиций И. т. можно рассматривать и различные явления в условиях плановой экономики (напр., вопросы централизации и децентрализации управления производством, преодоление ведомственных противоречий, оптимальное планирование по нескольким показателям, планирование в условиях неопределенности, порождаемой, напр., технич. прогрессом, и т. д.). Исторический очерк. Зарождение И. т. как математич. дисциплины можно отнести к тому же письму Б. Паскаля (В. Pascal) к П. Ферма (P. Fermat) от 29 июля 1654, к-рое принято считать началом математич. теории вероятностей. В дальнейшем отдельные идеи, к-рые можно отнести к теоретико-игровым, высказывались Вальдегравом (Waldegrave, 1712; нахождение оптимальных смешанных стратегий в игре "проходящий туз"), Д. Бернулли (D. Bernoulli, 1732; анализ "петербургской игры"), П. Лапласом (P. Laplace, 1814; рассмотрение принципов оптимальности) и Ж. Бертраном (J. Bertrand, 1888; теоретико-игровой подход к игре в бакара). Ряд по существу теоретико-игровых утверждений был в эквивалентной форме рассмотрен в других разделах математики: в теории наилучших приближений (П. Л. Чебышев), в геометрии выпуклых многогранников [Г. Минковский (Н. Minkowski)], в теории линейных неравенств [Э. Штимке (Е. Stiemke)]. В 1911 Э. Цермело (Е. Zermelo) описал теоретико-игровой подход к шахматной игре; в 1921 Э. Борель (Е. Borel) начал систематич. изучение матричных игр, доказав для нек-рых случаев существование оптимальных смешанных стратегий. В 1928 вышла в свет работа Дж. Неймана "К теории стратегических игр", содержащая основные идеи современной И. т. Эти идеи были детально разработаны Дж. Нейманом и О. Моргенштерном (О. Morgenstern, [1]). С тех пор И. т. вошла в число разделов современной математики. Лит.:[1] Нейман Дж., Моргенштерн О., Теория игр и экономическое поведение, пер. с англ., М., 1970; [2] Льюс Р., Райфа X., Игры и решения, пер. с англ., М., 1961: [3] Карлин С, Математические методы в теории игр, программировании и экономике, пер. с англ., М., 1964; [4] Воробьев Н. Н., "Успехи матем. наук", 1970, т. 15, в. 2, с. 80-140; [5] Оуэн Г., Теория игр., пер. с англ., М., 1971; [6] Партхасаратхи Т., Рагхаван Т., Некоторые вопросы теории игр двух лиц, пер. с англ., М., 1974; [7] Воробьев Н. Н., Теория игр. Лекции для экономистов-кибернетиков, Л., 1974; [8] его же, Entwicklung der Spieltheorie, В., 1975; [9] Теория игр. Аннотированный указатель публикаций по 1968 г., Л., 1976; [10] Журнал "International Journal of Game Theory", Vienna (выходит с 1971). H. H. Воробьев. |
|
|
|

 участвующих в нем действующих начал (называемых коалициями действи я), 2) семейство множеств rK стратегий каждой из коалиций действия, 3) множество ситуаций
участвующих в нем действующих начал (называемых коалициями действи я), 2) семейство множеств rK стратегий каждой из коалиций действия, 3) множество ситуаций  4). множество П U заинтересованных начал (называемых коалициями интересов) и 5) семейства бинарных отношений
4). множество П U заинтересованных начал (называемых коалициями интересов) и 5) семейства бинарных отношений  на
на  выражающих предпочтения между ситуациями для коалиций интересов. Система
выражающих предпочтения между ситуациями для коалиций интересов. Система
 Каждому игроку
Каждому игроку  ставится в соответствие координатная прямая Е i, принимаемая за шкалу его полезностей, а каждой коалиции интересов
ставится в соответствие координатная прямая Е i, принимаемая за шкалу его полезностей, а каждой коалиции интересов  - произведение
- произведение  Наконец, вводятся множества
Наконец, вводятся множества  для каждого
для каждого  и множество
и множество  (элементы к-рого наз. дележами) и по определению принимается, что для дележей х,
(элементы к-рого наз. дележами) и по определению принимается, что для дележей х,  имеет место
имеет место  ("дележ x доминирует дележ упо коалиции K") тогда и только тогда, когда х, у
("дележ x доминирует дележ упо коалиции K") тогда и только тогда, когда х, у (v(K)
(v(K)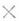 ХЕ I'K)
ХЕ I'K) Н и xi>yi для всех
Н и xi>yi для всех  Такие игры наз. играми без побочных платежей. Они описывают положение, при к-ром каждая коалиция интересов К может форсированно обеспечить для своих членов в качестве выигрышей компоненты любого вектора из v(K), а общие соображения целесообразности делают нерациональным выбор дележей вне Н. Обычно множества v(K)подчиняются нек-рым естественным условиям: 1) v(K)является непустым замкнутым и выпуклым множеством, 2) если
Такие игры наз. играми без побочных платежей. Они описывают положение, при к-ром каждая коалиция интересов К может форсированно обеспечить для своих членов в качестве выигрышей компоненты любого вектора из v(K), а общие соображения целесообразности делают нерациональным выбор дележей вне Н. Обычно множества v(K)подчиняются нек-рым естественным условиям: 1) v(K)является непустым замкнутым и выпуклым множеством, 2) если 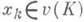 и
и (неравенство векторов понимается покомпонентно), то
(неравенство векторов понимается покомпонентно), то  ("кто способен на большее, способен и на меньшее"), 3) если
("кто способен на большее, способен и на меньшее"), 3) если  то
то  (коалиции Ки Lвместе могут добиться не меньшего, чем порознь), 4) Н состоит из всех таких векторов
(коалиции Ки Lвместе могут добиться не меньшего, чем порознь), 4) Н состоит из всех таких векторов  что для каждого из них найдется вектор
что для каждого из них найдется вектор  для к-рого
для к-рого  (таким образом, v{I )состоит из всех таких векторов выигрышей х, что I может дать своим членам не менее чем х; Н состоит из таких векторов х, что I может дать своим членам ровно х). В частности, если
(таким образом, v{I )состоит из всех таких векторов выигрышей х, что I может дать своим членам не менее чем х; Н состоит из таких векторов х, что I может дать своим членам ровно х). В частности, если

 и коалиций интересов
и коалиций интересов  Каждый игрокимеет
Каждый игрокимеет  в своем распоряжении множество стратегий
в своем распоряжении множество стратегий  в качестве множества всех ситуаций принимается декартово произведение
в качестве множества всех ситуаций принимается декартово произведение  а отношение предпочтения
а отношение предпочтения  описывается функцией выигрыша Hi:r->Ei причем
описывается функцией выигрыша Hi:r->Ei причем  тогда и только тогда, когда Н i( х')>Н i(x").
тогда и только тогда, когда Н i( х')>Н i(x").
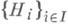 >.
>. конечны, то и бескоалиционная игра Г наз. конечной. Конечные бескоалиционные игры с двумя игроками (I={I, II}) наз. биматричными играми..
конечны, то и бескоалиционная игра Г наз. конечной. Конечные бескоалиционные игры с двумя игроками (I={I, II}) наз. биматричными играми.. то игра Г наз. антагонистической игрой. Всякая антагонистич. игра может быть задана в виде тройки
то игра Г наз. антагонистической игрой. Всякая антагонистич. игра может быть задана в виде тройки  где
где  и
и  - множества стратегий, соответственно, игроков I и II, а H - функция выигрыша игрока I. Конечные антагонистич. игры наз. матричными играми.
- множества стратегий, соответственно, игроков I и II, а H - функция выигрыша игрока I. Конечные антагонистич. игры наз. матричными играми. то всякая ситуация в такой игре описывается точкой из квадрата [0, 1]
то всякая ситуация в такой игре описывается точкой из квадрата [0, 1] [0, 1]; такие игры наз. играми на единичном квадрате.
[0, 1]; такие игры наз. играми на единичном квадрате. - множества их стратегий; X- множество, элементы к-рого наз. позициями; Т- множество, элементы к-рого имеют смысл моментов времени;
- множества их стратегий; X- множество, элементы к-рого наз. позициями; Т- множество, элементы к-рого имеют смысл моментов времени;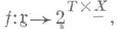 т. е. f ставит в соответствие каждой ситуации определяемой игры отношение, заданное на Тсо значениями в
т. е. f ставит в соответствие каждой ситуации определяемой игры отношение, заданное на Тсо значениями в  всякий f-образ ситуации наз. партией (множество всех партий обозначается через
всякий f-образ ситуации наз. партией (множество всех партий обозначается через  и, наконец,
и, наконец, Сиcтема
Сиcтема
 Х. Пусть рассматриваются ситуации
Х. Пусть рассматриваются ситуации  для которых система дифференциальных уравнений
для которых система дифференциальных уравнений
 (множество оптимальных в этом смысле ситуаций наз. с-ядром игры). Другой принцип оптимальности состоит в сочетании внутренней п внешней устойчивости; это означает, что множество ситуаций R объявляется решением, если при х,
(множество оптимальных в этом смысле ситуаций наз. с-ядром игры). Другой принцип оптимальности состоит в сочетании внутренней п внешней устойчивости; это означает, что множество ситуаций R объявляется решением, если при х, . и
. и  не может быть
не может быть  а по всякому xПR найдутся такие zОR и
а по всякому xПR найдутся такие zОR и  что
что  (такое Rназ. решением игры по Нейману - Моргенштерну). Можно формализовать Угрозы, предъявляемые одними коалициями другим, а также ответные контругрозы, и объявить устойчивой всякую ситуацию, в к-рой каждая угроза может парироваться контругрозой. Множество всех устойчивых в этом смысле ситуаций наз. k-я дро м игры. Представляет также интерес понимание оптимальности как своеобразной "справедливости", задаваемой нек-рой системой аксиом. Для кооперативных игр сформулирована такая аксиоматика, приводящая к единственному дележу (ситуации), называемому Шепли вектором. В стратегич. играх основой принципа оптимальности является идея равновесия. При этом оптимальными объявляются такие ситуации, отклонения от к-рых любым игроком не приводят к увеличению его выигрыша. Один и тот же принцип оптимальности, формулируемый для различных по объему классов игр, может приобретать различное содержательное выражение. Так, описанный принцип равновесия в случае антагонистич. игр превращается в минимакса принцип.
(такое Rназ. решением игры по Нейману - Моргенштерну). Можно формализовать Угрозы, предъявляемые одними коалициями другим, а также ответные контругрозы, и объявить устойчивой всякую ситуацию, в к-рой каждая угроза может парироваться контругрозой. Множество всех устойчивых в этом смысле ситуаций наз. k-я дро м игры. Представляет также интерес понимание оптимальности как своеобразной "справедливости", задаваемой нек-рой системой аксиом. Для кооперативных игр сформулирована такая аксиоматика, приводящая к единственному дележу (ситуации), называемому Шепли вектором. В стратегич. играх основой принципа оптимальности является идея равновесия. При этом оптимальными объявляются такие ситуации, отклонения от к-рых любым игроком не приводят к увеличению его выигрыша. Один и тот же принцип оптимальности, формулируемый для различных по объему классов игр, может приобретать различное содержательное выражение. Так, описанный принцип равновесия в случае антагонистич. игр превращается в минимакса принцип.