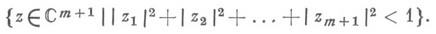ЗИГЕЛЯ ОБЛАСТЬ

Значение ЗИГЕЛЯ ОБЛАСТЬ в математической энциклопедии:

- неограниченная область в (гс+т)-мерном комплексном аффинном пространстве имеющая вид

где V- открытый выпуклый конус в пространстве Rⁿ,a F:C^mXC^m->Cⁿ- отображение, являющееся V- эрмитовой формой, а именно, Fлинейно по первому аргументу, (- замыкание V), F(w, w') = 0 только при w=0. В случае, когда т=0 (и, стало быть, F=0 )область D(V, F )наз. 3. о. первого рода и обозначается просто D(V);в случае, когда область D(V, F )наз. 3. о. второго рода.

Простейшим примером 3. о. (первого рода) является верхняя полуплоскость одного, комплексного переменного. В работе К. Зигеля [1] в связи с исследованием абелевых многообразий была рассмотрена область Н _р в пространстве комплексных симметричных матриц порядка р, образованная матрицами, мнимая часть к-рых положительно определена. Эта область, наз. теперь верхней полуплоскостью Зигеля (и при р=1 совпадающая с обычной верхней полуплоскостью), является 3. о. первого рода, ассоциированной с конусом положительно определенных симметричных матриц порядка р. Общее понятие 3. о. возникло в связи с изучением автоморфных функций многих комплексных переменных (см. [5]). Впоследствии это понятие стало центральным в теории однородных ограниченных областей.

Всякая 3. о. аналитически изоморфна ограниченной области. Напр., при n=1 3. о. изоморфна комплексному шару

Всякая однородная ограниченная область изоморфна 3. о., однородной относительно аффинных преобразований. Две 3. о. аналитически изоморфны тогда и только тогда, когда они переводятся одна в другую аффинным преобразованием (см. [3]).

Лит.:[1] Siegel С. L.,"Math. Ann.", 1939, Bd 116, S. 617- 57; [2] Зигель К., Автоморфные функции нескольких комплексных переменных, пер. с англ., М., 1954; [3] Каир W., Matsushima Y., Осhiai Т., "Amer. J. Math.", 1970, v. 92, p. 475-98; [4] Murakami S., On Automorphisms of Siegel Domains, B.- Hdlb.- N.Y., 1972; [5] Итоги науки. Матем. анализ. 1963, М., 1965, с. 81 - 124.

Э. Б. Винберг.