|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЗЕЙФЕРТА РАССЛОЕНИЕЗначение ЗЕЙФЕРТА РАССЛОЕНИЕ в математической энциклопедии: - класс расслоений трехмерных многообразий на окружности; определен X. Зейфертом [1]. Каждый слой 3. р. имеет в многообразии М 3 окрестность со стандартным расслоением на окружности, к-рое возникает из произведения D2 Образы отрезков х Геометрич. смысл a и b состоит в следующем: если в расслоении, индуцированном на крае Р, взять меридиан т. (кривая, стягиваемая в Р)и параллель I(пересекающую ттрансверсально один раз), а также любой слой f и секущую g(все четыре кривые простые и замкнутые), то при надлежащей ориентации
причем Первая задача относительно 3. р. состоит в их классификации с точностью до послойного гомеоморфизма. Оказывается [1], что если М 3 имеет 3. р., то существует отображение я:
так что с точностью до послойного гомеоморфизма имеется одно и только одно 3. р. с таким набором. Здесь e= О i или ni, р- род В 2,(ai, bi) - инварианты Зейферта для особых слоев расслоения, число к-рых равно r, причем Вторая задача относительно 3. р. заключается в установлении того, что на замкнутом многообразии М 3 может существовать не более одного такого расслоения с точностью до послойных гомеоморфизмов. Это доказано для так наз. больших 3. р., к-рые являются пространствами типа K(p, 1), т. е. гомотопич. тип к-рых определен фундаментальной группой. Фундаментальную группу p1( М 3 )многообразия, снабженного З. р., удобно описывать с помощью специальной системы образующих: сечений gj на краях окрестностей особых слоев, элементов а i, bi;(или vi;, если В 2 неориентируемо), образы к-рых в p1(B2) являются канонич. образующими, h- неособый слой. При этом определяющие соотношения в случаях О 1 и О 2 следующие:
а в случаях ni:
где ei=l в зависимости от того, обращается ли ориентация слоя при обносе вдоль соответствующей образующей p1( В 2). К многообразиям смалыми 3. р. относятся: для типа О 1 все расслоения с
для типа О 2 только расслоения с р=1, r=0; для типов n1 и n2 расслоения с р=1, п 3 расслоения с р = 2, r=0. Все 3. р. типа n4 большие. Малые 3. р. все перечислены, их имеется 10 типов (см. [3]). Свободные действия конечных групп на трехмерной сфере коммутируют с естественным действием на ней группы SO(2), и поэтому пространства орбит этих действий оказываются 3. р. с конечными фундаментальными группами. Это - единственные известные (1977) примеры М 3 с конечной p1( М 3). Heк-рые из 3. р. встречаются как границы сферич. окрестностей изолированных особых точек алгебраич. поверхностей, инвариантных относительно действия мультипликативной группы комплексных чисел. Именно, это 3. р. типа: {b; ( О 1, р); (a1, b1), ..., (ar, br)} при b+r>0. Идентификация этих многообразий, позволяет построить явное разрешение особенностей с учетом действия С* (а также дать полное описание изолированных особенностей поверхностей в С 3, допускающих действие С*). 3. р. имеются также на локально плоских римановых многообразиях, полученных при факторизации евклидова пространства по свободному действию дискретной группы движений (имеется 6 ориентированных и 4 неориентируемых многообразия, все из к-рых, кроме одного, являются различными расслоениями над окружностью со слоем тор или поверхность Клейна). В топологии трехмерных многообразий 3. р. важны, напр., для идентификации многообразий, фундаментальные группы к-рых имеют центр [4]. Имеются также обобщения 3. р. на другие классы расслоений с особыми слоями. Лит.:[l]Seifert H., "Acta Math.", 1933, Bd 60, S. 147- 238; [2] Holmann H., "Math. Ann.", 1964, Bd 157, S. 138-66; [3] Orlik P., Seifert manifolds, В.- Hdlh.-N. Y., 1972; [4] Hempel J., 3-manifolds, N.Y., 1976. А. В. Чернавский. |
|
|
|

 [0, 1] диска на отрезок при склейке каждой точки ( х,0) с точкой (g(x),1), где g- поворот D2 на угол 2pv/m (m и v - взаимно простые целые числа,
[0, 1] диска на отрезок при склейке каждой точки ( х,0) с точкой (g(x),1), где g- поворот D2 на угол 2pv/m (m и v - взаимно простые целые числа,  ).
). [0, 1] в полученном полнотории Рсоставляют слои: каждый слой, кроме централыгого, состоит из m отрезков; центральный слой наз. особым, если v>0. Инварианты (m, v) обычно заменяются инвариантами Зейферта (а, Р), где a=m, a b определяется
[0, 1] в полученном полнотории Рсоставляют слои: каждый слой, кроме централыгого, состоит из m отрезков; центральный слой наз. особым, если v>0. Инварианты (m, v) обычно заменяются инвариантами Зейферта (а, Р), где a=m, a b определяется 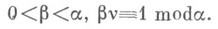 из условий
из условий

 где В 2 - двумерное многообразие, и слоями служат p-1 (х),
где В 2 - двумерное многообразие, и слоями служат p-1 (х), 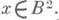 Имеется шесть типов 3. р.: типы О 1 и О 2, в к-рых В 2 ориентируемо и М 3 ориентируемо в случае O1 и неориентируемо в случае О 2, причем род В 2 в этом случае не меньше единицы, и типы ni, i=i,2, 3, 4, для к-рых В 2 неориентируемо. В случае n1 обнос слоя вдоль пути в В 2 не меняет ориентацию слоя, в случае п 2 имеется система образующих, обнос вдоль к-рых меняет ориентацию, в случае п 3 не меняет ориентацию только одна из образующих, а в случае n4 - только две из образующих, причем род В 2 не меньше двух для п 3 и не меньше трех для n4. Многообразие М 3 ориентируемо только для типа n2. Каждому 3. р. относится система инвариантов
Имеется шесть типов 3. р.: типы О 1 и О 2, в к-рых В 2 ориентируемо и М 3 ориентируемо в случае O1 и неориентируемо в случае О 2, причем род В 2 в этом случае не меньше единицы, и типы ni, i=i,2, 3, 4, для к-рых В 2 неориентируемо. В случае n1 обнос слоя вдоль пути в В 2 не меняет ориентацию слоя, в случае п 2 имеется система образующих, обнос вдоль к-рых меняет ориентацию, в случае п 3 не меняет ориентацию только одна из образующих, а в случае n4 - только две из образующих, причем род В 2 не меньше двух для п 3 и не меньше трех для n4. Многообразие М 3 ориентируемо только для типа n2. Каждому 3. р. относится система инвариантов
 в случаях e=О2, п1,n3, n4, и, наконец, b- целое число, если e=O1 или п г и вычет mod2 в остальных случаях, при этом b=0, если ai= 2 хотя бы для одного слоя. Геометрич. смысл b:на крае окрестности каждого особого слоя выбирается сечение, и вся их совокупность продолжается до сечения во всем дополнении к особым слоям. Это возможно сделать вплоть до одного неособого слоя, к к-рому край продолжаемого сечения подойдет, накручиваясь на него со степенью b. При изменении ориентации М 3 в случаях О 1 и n2 число b меняется на -b-r, а bi - на ai-bi.
в случаях e=О2, п1,n3, n4, и, наконец, b- целое число, если e=O1 или п г и вычет mod2 в остальных случаях, при этом b=0, если ai= 2 хотя бы для одного слоя. Геометрич. смысл b:на крае окрестности каждого особого слоя выбирается сечение, и вся их совокупность продолжается до сечения во всем дополнении к особым слоям. Это возможно сделать вплоть до одного неособого слоя, к к-рому край продолжаемого сечения подойдет, накручиваясь на него со степенью b. При изменении ориентации М 3 в случаях О 1 и n2 число b меняется на -b-r, а bi - на ai-bi.


 р=2, r=0; для типа
р=2, r=0; для типа