"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЗАРИСКОГО ТЕОРЕМАЗначение ЗАРИСКОГО ТЕОРЕМА в математической энциклопедии:
о связности: пусть f:  - собственный сюръективный морфизм неприводимых многообразий и пусть поле рациональных функций k(Y)сепарабельно алгебраически замкнуто в k(Х), а - собственный сюръективный морфизм неприводимых многообразий и пусть поле рациональных функций k(Y)сепарабельно алгебраически замкнуто в k(Х), а 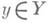 -нормальная точка, тогда f-1(y)связно (и более того, геометрически связно) (см. [2]). Эта теорема обосновывает классический 1 принцип вырождения: если общий цикл алгебраич. системы циклов является многообразием (т. е. геометрически неприводим), то любая специализация этого цикла связна. -нормальная точка, тогда f-1(y)связно (и более того, геометрически связно) (см. [2]). Эта теорема обосновывает классический 1 принцип вырождения: если общий цикл алгебраич. системы циклов является многообразием (т. е. геометрически неприводим), то любая специализация этого цикла связна. Частным случаем 3. т. о связности является так наз. основная теорема Зариского, или теорема Зариского о бирациональных соответствиях: бирациональный морфизм алгебраич. многообразий /: является открытым вложением в окрестности нормальной точки является открытым вложением в окрестности нормальной точки  если f -1(y)- конечное множество (см. [1]). В частности, бирациональный морфизм нормальных многообразий, биективный на точках, является изоморфизмом. Другая формулировка этой теоремы: пусть f: если f -1(y)- конечное множество (см. [1]). В частности, бирациональный морфизм нормальных многообразий, биективный на точках, является изоморфизмом. Другая формулировка этой теоремы: пусть f: - квазиконечный отделимый морфизм схем, а У - квазикомпактная квазиотделимая схема, тогда существует разложение f= uog, где и- конечный морфизм, a g- открытое вложение [3]. - квазиконечный отделимый морфизм схем, а У - квазикомпактная квазиотделимая схема, тогда существует разложение f= uog, где и- конечный морфизм, a g- открытое вложение [3]. Лит.:[1] Zariski О., "Trans. Amer. Math. Soc", 1943, v. 53, № 3, p. 490-542; [2] eго же, "Mem. Amer. Math. Soc", 1951, № 5, p. 1-90; [3] Grоthendieсk A., "Publ. Math. IHES", 1961, № 11; 1967, K"32. В. И. Данилов.
|

 - собственный сюръективный морфизм неприводимых многообразий и пусть поле рациональных функций k(Y)сепарабельно алгебраически замкнуто в k(Х), а
- собственный сюръективный морфизм неприводимых многообразий и пусть поле рациональных функций k(Y)сепарабельно алгебраически замкнуто в k(Х), а 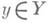 -нормальная точка, тогда f-1(y)связно (и более того, геометрически связно) (см. [2]). Эта теорема обосновывает классический 1 принцип вырождения: если общий цикл алгебраич. системы циклов является многообразием (т. е. геометрически неприводим), то любая специализация этого цикла связна.
-нормальная точка, тогда f-1(y)связно (и более того, геометрически связно) (см. [2]). Эта теорема обосновывает классический 1 принцип вырождения: если общий цикл алгебраич. системы циклов является многообразием (т. е. геометрически неприводим), то любая специализация этого цикла связна. является открытым вложением в окрестности нормальной точки
является открытым вложением в окрестности нормальной точки  если f -1(y)- конечное множество (см. [1]). В частности, бирациональный морфизм нормальных многообразий, биективный на точках, является изоморфизмом. Другая формулировка этой теоремы: пусть f:
если f -1(y)- конечное множество (см. [1]). В частности, бирациональный морфизм нормальных многообразий, биективный на точках, является изоморфизмом. Другая формулировка этой теоремы: пусть f: - квазиконечный отделимый морфизм схем, а У - квазикомпактная квазиотделимая схема, тогда существует разложение f= uog, где и- конечный морфизм, a g- открытое вложение [3].
- квазиконечный отделимый морфизм схем, а У - квазикомпактная квазиотделимая схема, тогда существует разложение f= uog, где и- конечный морфизм, a g- открытое вложение [3].