|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЗАМКНУТАЯ СИСТЕМАЗначение ЗАМКНУТАЯ СИСТЕМА в математической энциклопедии: элементов, замкнутая система функций,- система элементов jn некоторого линейного нормированного пространства Нтакая, что любой элемент
Напр., система степеней { х п}, n=0, 1, 2, ..., замкнута в пространстве Lp[a, b, dm(x)]. функций, суммируемых в степени
где Qn(x)- многочлен степени п. Обычно рассматривается случай, когда {jn} - ортонормированная последовательность элементов в гильбертовом пространстве Н.*Тогда условие замкнутости (1) эквивалентно выполнению для всех элементов
где { а п }- коэффициенты Фурье элемента f по системе {jn}. В случае тригонометрич. системы функций условие (3) наз. равенством Парсеваля; оно имеет вид
Это равенство рассматривали М. Парсеваль (М. Раrseval, 1806), Ш. Балле Пуссен (Ch. La Vallee Poussin, 1890), А. Гурвиц (A. Hurwitz, 1901-03); строгое его доказательство дал (в случае, когда f(x)ограничена) А. М. Ляпунов (1896). Общий случай условия замкнутости (3) впервые подробно исследовал В. А. Стеклов (1898) в связи с решением нек-рых задач математич. физики. Введя термин "замкнутость", В. А. Стеклов рассмотрел с этой точки зрения различные конкретные системы ортогональных функций, и в частности фундаментальные решения уравнения Штурма - Лиувилля (см. Штурма- Лиувилля задача). Поэтому равенство (3) часто наз. условием замкнутости Парсеваля - Стеклова. Понятие замкнутости широко применяется в теории ортогональных многочленов. Если отрезок ортогональности конечен, то система ортогональных многочленов замкнута при любом весе. В случае бесконечного интервала ортогональности В. А. Стеклов установил ряд условий на весовую функцию, достаточных для замкнутости соответствующей системы ортогональных многочленов: в частности, он доказал замкнутость систем многочленов Эрмита и Лагерра. Одно из достаточных условий Стеклова в случав интервала
где h(x)- дифференциальный вес на интервале
Это условие в нек-ром смысле близко к необходимому, ибо, как показал еще В. А. Стеклов, система многочленов незамкнута в случае весовой функции вида
Полное решение вопроса об условиях замкнутости системы многочленов в пространстве L2[a, b, dm(x)]в случае бесконечного интервала дал М. Рис (М. Riesz, 1922). Он доказал, что для замкнутости системы многочленов в L2 [a, b, dm(x)]необходимо и достаточно, чтобы либо соответствующая моментов проблема была определенной, либо в случае неопределенности функция m(х)была так наз. N-экстремальным решением проблемы моментов. С понятием замкнутости тесно связано понятие полноты системы функций, к-рое заключается в том, что из равенства нулю линейного ограниченного функционала f на всех элементах системы {j п} следует условие f=0. В гильбертовом пространстве эти два понятия эквивалентны. Полнота системы {j п (х)} в пространстве Lp эквивалентна замкнутости этой же системы в Lq, где
В комплексной области подробно изучены аналоги неравенств типа (1) или (2) для систем многочленов и более общих систем функций (см. Ортогональные многочлены в комплексной области). Лит.:[1]Качмаж С, Штейнгауз Г., Теория ортогональных рядов, пер. снем.,М., 1958; [2] Геронимус Я. <Л., Теория ортогональных многочленов. Обзор достижений отечественной математики, М.- Л., 1950; [3] Сегё Г., Ортогональные многочлены, пер. с англ., М., 1962; [4] Стеклов В. А., "Зап Акад. наук" (физ.-матем. сер.), 1911, т. 30, № 4, с 1-86; 1914, т. 33, № 8, с. 1-59; [5] его же, Основные задачи математической физики, ч. 1-2, П., 1922-23; [6] Riеsz М., в кн.: Acta litterarumac Scientiarum regial Universitatis Hungaricae. Sec. scient. mathemat., 1922-1923, kot. 1, old. .209-25; [7] Hewitt E.,"Amer. Math. Monthly", 1954, v. 61, p. 249 - 50. П. К. Суетин. |
|
|
|

 можно сколь угодно точно приблизить в метрике пространства Нконечной линейной комбинацией элементов из этой системы, т. е. для всякого e>0 найдутся такие числа с 0, с 1 ..., с п, что выполняется неравенство
можно сколь угодно точно приблизить в метрике пространства Нконечной линейной комбинацией элементов из этой системы, т. е. для всякого e>0 найдутся такие числа с 0, с 1 ..., с п, что выполняется неравенство
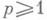 на конечном отрезке [ а, b]с интегральным весом m(x), причем неравенство (1) в этом случае имеет вид
на конечном отрезке [ а, b]с интегральным весом m(x), причем неравенство (1) в этом случае имеет вид
 равенств
равенств

 заключается в том, что существует такая последовательность положительных чисел {а п), для к-рой выполняются соотношения
заключается в том, что существует такая последовательность положительных чисел {а п), для к-рой выполняются соотношения
 (т. е. dm(x) = h(x)dx). Для всего интервала
(т. е. dm(x) = h(x)dx). Для всего интервала  достаточное условие состоит в том, чтобы дифференциальный вес h(х)был почти всюду положителен п удовлетворял неравенству
достаточное условие состоит в том, чтобы дифференциальный вес h(х)был почти всюду положителен п удовлетворял неравенству