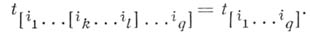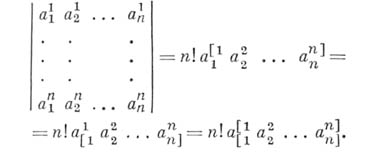|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
АЛЬТЕРНИРОВАНИЕЗначение АЛЬТЕРНИРОВАНИЕ в математической энциклопедии: кососимметрирование, антисимметрирован не, альтернация, - одна пэ операций тензорной алгебры, при помощи к-рой по данному тензору строится ко-сосимметрический (по группе индексов) тензор. А. всегда производится по нескольким верхним или нижним индексам. Тензор Здесь суммирование производится по всем А. по группе индексов обозначается взятием этих индексов в квадратные скобки. Посторонние индексы, попавшие внутрь квадратных скобок, отделяются вертикальными черточками. Напр., Последовательное А. по группам индексов Если п - размерность векторного пространства, в к-ром определен тензор, то А. по группе индексов, количество к-рых больше п, всегда дает нулевой тензор. А. по нек-рой группе индексов тензора, симметричного (см. Симметрирование).по этой группе, также дает нулевой тензор. Тензор, не изменяющийся при. А. по нек-рой группе индексов I, наз. кососимметрическим, или альтернированным, по группе индексов I. Перестановка любой пары таких индексов ведет к изменению знака у координаты тензора. Операция А. тензора, наряду с операцией симметрирования, применяется для разложения тензора на более простые тензоры. Произведение двух тензоров с последующей А. по всем индексам наз. альтернированным произведением (внешним произведением). А. применяется также для образования знакопеременных (альтернированных) сумм вида (*) с многоиндексными слагаемыми. Напр., вычисление определителя (с коммутирующими при умножении элементами) производится по следующим формулам: Лит.:[1] Широков П. А., Тензорное исчисление, 2 изд., Казань, 1961; [2] Беклемишев Д. В., Курс аналитической геометрии и линейной алгебры, М., 1971; [3] Схоутен Я. А., Тензорный анализ для физиков, пер. с англ., М., 1965; [4] Ефимов Н. В., Розендорн Э. Р., Линейная алгебра и многомерная геометрия, М., 1970. Л. П. Купцов. |
|
|
|

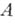 с координатами
с координатами 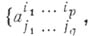
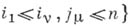 является результатом А. тензора
является результатом А. тензора  с координатами
с координатами 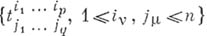 по верхним индексам, напр., по группе индексов I=(i1 , i2 , ...,im). если
по верхним индексам, напр., по группе индексов I=(i1 , i2 , ...,im). если 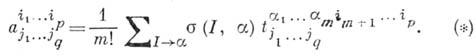
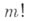 перестановкам
перестановкам 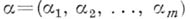 группы индексов
группы индексов 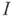 , а число
, а число 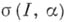 равно
равно 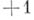 или
или 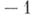 , если соответствующая перестановка четна или нечетна. Аналогично определяется А. по группе нижних индексов.
, если соответствующая перестановка четна или нечетна. Аналогично определяется А. по группе нижних индексов.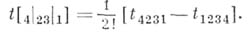
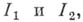
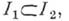 совпадает с А. по группе индексов
совпадает с А. по группе индексов 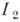 :
: