|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЗАВИСЯЩИЙ ОТ ПАРАМЕТРОВ ИНТЕГРАЛЗначение ЗАВИСЯЩИЙ ОТ ПАРАМЕТРОВ ИНТЕГРАЛ в математической энциклопедии: - интеграл вида
в к-ром точка х=(x1, х 2, ..., х п )пробегает пространство Rn (в случае, если эта точка пробегает только нек-рую область Dв пространстве Rn, то функцию f(x, у )можно считать равной нулю при Основные вопросы теории таких интегралов - это выяснение условий непрерывности и дифференцируемости функции J(y)по параметрам у 1, у 2, ..., у m.Менее стеснительные условия непрерывности и дифференцируемости J(у)получают при понимании интеграла в смысле Лебега. Справедливы следующие утверждения. 1) Если функция f(x, у )для почти всех 2) Если функция f(x, t), определенная при
следует дифференцйруемость по tна интервале ( а, b )функции
и возможность вычисления производной J'(t)дифференцированием под знаком интеграла:
Из 1)- 2) получают ряд более простых утверждений о непрерывности и дифференцируемости интегралов по параметрам, относящихся к трактовке интеграла в смысле Римана и более частным случаям (см. [2] - [4]). Несобственные интегралы, зависящие от параметров. Для простейшего несобственного интеграла 1-го рода
вводят понятие равномерной сходимости по параметру tна нек-ром сегменте
для всех Справедливы следующие утверждения: а)Если функция f(x, t )непрерывна в полуполосе б) Если f(x, t )и производная
сходится равномерно относительно t на сегменте [ с, d], то функция J(t)дифференцируема на сегменте [ с, d]и ее производная может быть найдена по формуле
Аналогичные утверждения справедливы и для несобственного интеграла 2-го рода. Лит.:[1] Владимиров В. С, Уравнения математической физики, 2 изд., М., 1971; [2] Ильин В. А., Позняк Э. Г., Основы математического анализа, ч. 2, М., 1973; [3] Кудрявцев Л. Д., Математический анализ, т. 2, М., 1970; [4] Никольский С. М., Курс математического анализа, т. 2, М., 1973; [5] Тихонов А. Н., Самарский А. А., Уравнения математической физики, 4 изд., М., 1972. В. А. Ильин. |
|
|
|


 а точка у=(y1, у 2, ..., у т), образующая совокупность параметров у 1, у 2, ..., у т, изменяется в пределах нек-рой области Gпространства Rm.
а точка у=(y1, у 2, ..., у т), образующая совокупность параметров у 1, у 2, ..., у т, изменяется в пределах нек-рой области Gпространства Rm. непрерывна по ув области
непрерывна по ув области  и если существует интегрируемая в Rn функция g(x)такая, что для каждого
и если существует интегрируемая в Rn функция g(x)такая, что для каждого  и для почти всех
и для почти всех  справедливо неравенство
справедливо неравенство  то интеграл J(y)является непрерывной функцией ув области G.
то интеграл J(y)является непрерывной функцией ув области G.
 для почти всех
для почти всех  и каждого
и каждого  имеет производную
имеет производную  к-рая для почти каждого
к-рая для почти каждого  является непрерывной функцией tна интервале (а, 6), и если существует интегрируемая в Rn функция g(x)такая, что для каждого
является непрерывной функцией tна интервале (а, 6), и если существует интегрируемая в Rn функция g(x)такая, что для каждого  и для почти всех
и для почти всех  справедливо неравенство
справедливо неравенство  то из существования при нек-ром
то из существования при нек-ром 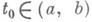 интеграла
интеграла
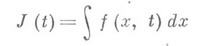

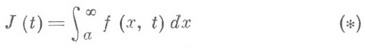
 Этот интеграл наз. равномерно сходящимся по tна сегменте [ с, d], если для любого e>0 найдется A(e)>0 такое, что
Этот интеграл наз. равномерно сходящимся по tна сегменте [ с, d], если для любого e>0 найдется A(e)>0 такое, что
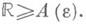
 и интеграл (*) сходится равномерно по tна сегменте [ с, d], то функция J(t)непрерывна на сегменте
и интеграл (*) сходится равномерно по tна сегменте [ с, d], то функция J(t)непрерывна на сегменте 
 непрерывны в полуполосе
непрерывны в полуполосе  интеграл (1) сходится для нек-рого
интеграл (1) сходится для нек-рого  а интеграл
а интеграл
