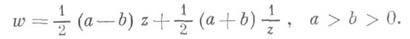|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЖУКОВСКОГО ФУНКЦИЯЗначение ЖУКОВСКОГО ФУНКЦИЯ в математической энциклопедии: - рациональная функция комплексного переменного z:
Важна своими применениями в гидромеханике, открытыми Н. Е. Жуковским (см. [1], [2]) в основном для построения п изучения профиля Жуковского (крыла Жуковского). Пусть в плоскости z заданы окружность К, проходящая через точки
и изображенная на рис. 2,- это и есть профиль Жуковского. Функция w=l(rt+a)отображает внешность единичного круга плоскости tна внешность V. Для получения профилей Жуковского более общего вида и расположения применяется обобщенная Ж. ф. (см. [3], [4], [5]):
Лит.:[1] Жуковский Н. Е., Гидродинамика, Собр. соч., М.-Л., т. 2, 1949; [2] его же, Теоретические основы воздухоплавания, Собр. соч., т. 6, 1950; [3] Маркушевич А. И., Теория аналитических функций, 2 изд., т. 1 - 2, М., 1967-68; [4] Седов Л. И., Плоские задачи гидродинамики и аэродинамики, 2 изд., М., 1966; [5] Кочин Н. Е., Кибель И А , Розе Н. В., Теоретическая гидромеханика, ч. 1, 6 изд., М., 1963. Е. Д. Соломенцев. |
|
|
|
(рис. 1), и окружность К', касающаяся Кизвне в точке z-1, с центром a. и радиусом r. При отображении w = k(z)образом окружности К' является нек-рая замкнутая кривая L' с острием в точке w=1, касающаяся в этой точке дугиокружности L(образа К)
