|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ЖЕСТКОЕ АНАЛИТИЧЕСКОЕ ПРОСТРАНСТВОЗначение ЖЕСТКОЕ АНАЛИТИЧЕСКОЕ ПРОСТРАНСТВО в математической энциклопедии: - вариант понятия аналитич. ространства, относящийся к случаю, когда основное поле Кявляется полным неархимедово нормированным полем. Аналитич. функции р-адического переменного рассматривались еще в конце 19 в. в теории алгебраич. чисел, однако соответствующий глобальный объект - Ж. а. п.- был введен Дж. Тейтом(1. Tate) лишь в начале 60-х гг. 20 в. (см. [1]). Этой конструкции предшествовало более прямолинейное построение по образцу теории комплексно аналитич. многообразий. Главный недостаток последнего подхода связан с тем, что обычное локальное определение аналитич. функции, как разлагающейся в степенной ряд в окрестности каждой точки, неудобно в силу полной несвязности основного поля К. Определенных таким образом аналитич. функций оказывалось "слишком много" (а аналитич. многообразий, соответственно, "слишком мало"). Напр., всякое компактное аналитич. многообразие над Кявляется объединением конечного множества замкнутых шаров (см. [3], с. 168). Конструкция Тейта начинается с выбора локальных объектов - аффиноидных пространств, аналогичных аффинным многообразиям в алгебраич. геометрии. Пусть Т п - алгебра степенных рядов от ппеременных t1,..., tn над К, сходящихся в полидиске Факторалгебры алгебры Т п наз. аффиноидными алгебрами. Эти алгебры нётеровы и в них имеется естественная банахова топология, в к-рой все идеалы замкнуты, а гомоморфизмы непрерывны. Оказывается, что любой максимальный идеал такой алгебры имеет конечную коразмерность и пространство МахA максимальных идеалов состоит, с точностью до сопряжения, из геометрич. точек, определенных над конечными расширениями поля К. В частности, МахTn есть полидиск единичного радиуса, а вообще, для произвольного Апространство МахA представляет собой аналитическое подмножество в полидиске. Гомомбрфизмы j: Жесткостью на топологич. пространстве Xназ. набор Т,CovU, QX, где Тесть семейство открытых множеств из X, называемых допустимыми, CovU для каждого Для Ж. а. п. получен ряд результатов, аналогичных известным теоремам теории комплексных пространств. Так, имеют место аналоги теорем Аи ВКартана (см. Картана теорема[4]). Точнее, когерентные пучки Лит.:[1] Тэйт Дж., "Математика", 1969, т. 13, №3, с. 3-37; [2] Бурбаки Н., Дифференцируемые и аналитические многообразия. Сводка результатов, пер. с франц., М., 1975; [3] Серр Ж.-П., Алгебры Ли и группы Ли, пер. с англ. и франц., М., 1969; [4] Узель К., "Математика", 1969, т. 13, № 3, с. 38-49; [5] Итоги науки и техники. Современные проблемы математики, т. 3, М., 1974, с. 5-92. А. Н. Паршин. |
|
|
|


 определяют морфизмы j*:
определяют морфизмы j*: так что аффиноидные пространства образуют категорию.
так что аффиноидные пространства образуют категорию. - семейства покрытий множества Uдопустимыми множествами (допустимые покрытия), а
- семейства покрытий множества Uдопустимыми множествами (допустимые покрытия), а 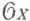 - предпучок колец на Т. Для допустимых покрытий требуется выполнимость естественных аксиом, в частности допустимые покрытия можно измельчать, а предпучок
- предпучок колец на Т. Для допустимых покрытий требуется выполнимость естественных аксиом, в частности допустимые покрытия можно измельчать, а предпучок  должен быть пучком относительно всех допустимых покрытий допустимых множеств. Морфизмы пространств с жесткостью, а также понятие индуцированной на подпространстве жесткости определяются по аналогии с такими же понятиями для окольцованных пространств. Каждое аффиноидное пространство можно наделить канонической жесткостью, сохраняющейся при любых морфизмах. Жесткое аналитическое пространство есть, по определению, топологич. пространство с жесткостью, на к-ром существует допустимое покрытие
должен быть пучком относительно всех допустимых покрытий допустимых множеств. Морфизмы пространств с жесткостью, а также понятие индуцированной на подпространстве жесткости определяются по аналогии с такими же понятиями для окольцованных пространств. Каждое аффиноидное пространство можно наделить канонической жесткостью, сохраняющейся при любых морфизмах. Жесткое аналитическое пространство есть, по определению, топологич. пространство с жесткостью, на к-ром существует допустимое покрытие  такое, что каждое X;с индуцированной жесткостью изоморфно аффиноидному пространству, наделенному канонич. жесткостью.
такое, что каждое X;с индуцированной жесткостью изоморфно аффиноидному пространству, наделенному канонич. жесткостью.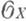 -модулей на аффиноидных пространствах однозначно определяются модулем своих сечений, а их когомологии в размерностях
-модулей на аффиноидных пространствах однозначно определяются модулем своих сечений, а их когомологии в размерностях  обращаются в нуль. Верен также аналог теоремы Грауэрта о когерентности прямого образа когерентного пучка при собственном отображении (однако определение собственного отображения здесь сильно отличается от обычного). Построен р-адический аналог униформизации алгебраических кривых и абелевых многообразий (см, [5]). Обнаружена связь между понятием Ж. а. п. и понятием формальной схемы в алгебраич. геометрии (см. [5]).
обращаются в нуль. Верен также аналог теоремы Грауэрта о когерентности прямого образа когерентного пучка при собственном отображении (однако определение собственного отображения здесь сильно отличается от обычного). Построен р-адический аналог униформизации алгебраических кривых и абелевых многообразий (см, [5]). Обнаружена связь между понятием Ж. а. п. и понятием формальной схемы в алгебраич. геометрии (см. [5]).