"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
АБЕЛЯ - ГОНЧАРОВА ПРОБЛЕМА
Значение АБЕЛЯ - ГОНЧАРОВА ПРОБЛЕМА в математической энциклопедии:
проблема Гончарова, - проблема в теории функций комплексного переменного, состоящая в нахождении множества всех функций  из того или иного класса, удовлетворяющих соотношениям
из того или иного класса, удовлетворяющих соотношениям  где
где  - допустимые для данного класса последовательности комплексных чисел. Эта проблема была поставлена В. Л. Гончаровым (см. [2]). Функции
- допустимые для данного класса последовательности комплексных чисел. Эта проблема была поставлена В. Л. Гончаровым (см. [2]). Функции  ставится в соответствие ряд
ставится в соответствие ряд

- интерполяционный ряд Абеля-Гончарова, где  - полином Гончарова, определяемый равенствами:
- полином Гончарова, определяемый равенствами:

Случай, когда  - действительные числа
- действительные числа  с формальной точки зрения рассмотрен Н. Абелем
с формальной точки зрения рассмотрен Н. Абелем  . Здесь
. Здесь

Ряд (*) является инструментом для изучения нулей последовательных производных регулярных функций. Множество функций  представимых рядом (*), наз. классом сходимости А.- Г. п.
представимых рядом (*), наз. классом сходимости А.- Г. п.
В случае был выделен класс сходимости А.- Г. п. в  терминах ограничений на порядок и тип целых функций /(z) в зависимости от роста величины
терминах ограничений на порядок и тип целых функций /(z) в зависимости от роста величины  (см. [2]).
(см. [2]).
В случае  где
где  - медленно растущая функция,
- медленно растущая функция,  был получен в нек-ром смысле точный класс сходимости А.- Г. п. (см. [6]). Были выделены также классы сходимости А.- Г. п. для целых функций конечного и бесконечного порядков в терминах различных ограничений, наложенных на индикаторы соответствующих классов функций; рассмотрена А.- Г. п. для целых функций многих переменных. Для нек-рого класса узлов интерполяции получены точные оценки полиномов Гончарова.
был получен в нек-ром смысле точный класс сходимости А.- Г. п. (см. [6]). Были выделены также классы сходимости А.- Г. п. для целых функций конечного и бесконечного порядков в терминах различных ограничений, наложенных на индикаторы соответствующих классов функций; рассмотрена А.- Г. п. для целых функций многих переменных. Для нек-рого класса узлов интерполяции получены точные оценки полиномов Гончарова.
Пусть  - класс функций f(z) вида
- класс функций f(z) вида

 - класс всевозможных последовательностей
- класс всевозможных последовательностей  таких, что
таких, что 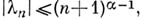 n= 0,1,.... Границей сход и мости для класса La наз. верхняя грань
n= 0,1,.... Границей сход и мости для класса La наз. верхняя грань  тех значений r, для к-рых всякая функция
тех значений r, для к-рых всякая функция  представима рядом (*). Нижняя грань
представима рядом (*). Нижняя грань  тех r, для к-рых существуют функция
тех r, для к-рых существуют функция  и последовательность
и последовательность  такие, что
такие, что  наз. границей единственности. Величины
наз. границей единственности. Величины  наз. соответственно константами Уиттекера и Гончарова. Было показано, что
наз. соответственно константами Уиттекера и Гончарова. Было показано, что  (см. [6]); доказаны также более общие утверждения:
(см. [6]); доказаны также более общие утверждения:

(см. [5], [10]).
Таким образом, при  А.- Г. п. сводится к нахождению константы
А.- Г. п. сводится к нахождению константы  Ее точное числовое значение неизвестно, однако найдены оценки: 0,7259<W1<0,7378 (см. [9]).
Ее точное числовое значение неизвестно, однако найдены оценки: 0,7259<W1<0,7378 (см. [9]).
При рассмотрении А.- Г. п. в классе  функций, регулярных в области
функций, регулярных в области  и таких, что
и таких, что  было показано, что для любого множества чисел
было показано, что для любого множества чисел 
 удовлетворяющих условию
удовлетворяющих условию

где  - возрастающая подпоследовательность натуральных чисел, из равенств
- возрастающая подпоследовательность натуральных чисел, из равенств 
следует  Причем для любого числа b>0 cуществуют последовательность
Причем для любого числа b>0 cуществуют последовательность 

и функция  для к-рых
для к-рых 
 (см.[7]).
(см.[7]).
А.- Г. п. включает так наз. задачу о двух точках, поставленную Э. Уиттекером (см. [12]). Пусть последовательности  таковы, что
таковы, что 
 Задача состоит в выяснении условий, при к-рых существует регулярная на отрезке [0, 1] функция
Задача состоит в выяснении условий, при к-рых существует регулярная на отрезке [0, 1] функция  удовлетворяющая условиям
удовлетворяющая условиям  Эта задача решалась в различных подклассах класса функций, регулярных в круге
Эта задача решалась в различных подклассах класса функций, регулярных в круге 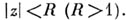 Полученные в нек-ром смысле точные условия выражены в терминах различных ограничений, наложенных на коэффициенты avk разложений
Полученные в нек-ром смысле точные условия выражены в терминах различных ограничений, наложенных на коэффициенты avk разложений

в зависимости от 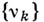 (см. [3]). Эта задача была обобщена, для решения ее были использованы методы теории бесконечных систем линейных уравнений (см. [4]). В частном случае, когда последовательность
(см. [3]). Эта задача была обобщена, для решения ее были использованы методы теории бесконечных систем линейных уравнений (см. [4]). В частном случае, когда последовательность  образует арифметич. прогрессию для целых функций экспоненциального типа, задача о двух точках в известном смысле решена до конца (см. [8]).
образует арифметич. прогрессию для целых функций экспоненциального типа, задача о двух точках в известном смысле решена до конца (см. [8]).


 из того или иного класса, удовлетворяющих соотношениям
из того или иного класса, удовлетворяющих соотношениям  где
где  - допустимые для данного класса последовательности комплексных чисел. Эта проблема была поставлена В. Л. Гончаровым (см. [2]). Функции
- допустимые для данного класса последовательности комплексных чисел. Эта проблема была поставлена В. Л. Гончаровым (см. [2]). Функции  ставится в соответствие ряд
ставится в соответствие ряд 
 - полином Гончарова, определяемый равенствами:
- полином Гончарова, определяемый равенствами:
 - действительные числа
- действительные числа  с формальной точки зрения рассмотрен Н. Абелем
с формальной точки зрения рассмотрен Н. Абелем  . Здесь
. Здесь 
 представимых рядом (*), наз. классом сходимости А.- Г. п.
представимых рядом (*), наз. классом сходимости А.- Г. п. терминах ограничений на порядок и тип целых функций /(z) в зависимости от роста величины
терминах ограничений на порядок и тип целых функций /(z) в зависимости от роста величины  (см. [2]).
(см. [2]). где
где  - медленно растущая функция,
- медленно растущая функция,  был получен в нек-ром смысле точный класс сходимости А.- Г. п. (см. [6]). Были выделены также классы сходимости А.- Г. п. для целых функций конечного и бесконечного порядков в терминах различных ограничений, наложенных на индикаторы соответствующих классов функций; рассмотрена А.- Г. п. для целых функций многих переменных. Для нек-рого класса узлов интерполяции получены точные оценки полиномов Гончарова.
был получен в нек-ром смысле точный класс сходимости А.- Г. п. (см. [6]). Были выделены также классы сходимости А.- Г. п. для целых функций конечного и бесконечного порядков в терминах различных ограничений, наложенных на индикаторы соответствующих классов функций; рассмотрена А.- Г. п. для целых функций многих переменных. Для нек-рого класса узлов интерполяции получены точные оценки полиномов Гончарова. - класс функций f(z) вида
- класс функций f(z) вида 
 - класс всевозможных последовательностей
- класс всевозможных последовательностей  таких, что
таких, что 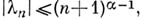 n= 0,1,.... Границей сход и мости для класса La наз. верхняя грань
n= 0,1,.... Границей сход и мости для класса La наз. верхняя грань  тех значений r, для к-рых всякая функция
тех значений r, для к-рых всякая функция  представима рядом (*). Нижняя грань
представима рядом (*). Нижняя грань  тех r, для к-рых существуют функция
тех r, для к-рых существуют функция  и последовательность
и последовательность  такие, что
такие, что  наз. границей единственности. Величины
наз. границей единственности. Величины  наз. соответственно константами Уиттекера и Гончарова. Было показано, что
наз. соответственно константами Уиттекера и Гончарова. Было показано, что  (см. [6]); доказаны также более общие утверждения:
(см. [6]); доказаны также более общие утверждения:
 А.- Г. п. сводится к нахождению константы
А.- Г. п. сводится к нахождению константы  Ее точное числовое значение неизвестно, однако найдены оценки: 0,7259<W1<0,7378 (см. [9]).
Ее точное числовое значение неизвестно, однако найдены оценки: 0,7259<W1<0,7378 (см. [9]). функций, регулярных в области
функций, регулярных в области  и таких, что
и таких, что  было показано, что для любого множества чисел
было показано, что для любого множества чисел 
 удовлетворяющих условию
удовлетворяющих условию 
 - возрастающая подпоследовательность натуральных чисел, из равенств
- возрастающая подпоследовательность натуральных чисел, из равенств 
 Причем для любого числа b>0 cуществуют последовательность
Причем для любого числа b>0 cуществуют последовательность 

 для к-рых
для к-рых 
 (см.[7]).
(см.[7]). таковы, что
таковы, что 
 Задача состоит в выяснении условий, при к-рых существует регулярная на отрезке [0, 1] функция
Задача состоит в выяснении условий, при к-рых существует регулярная на отрезке [0, 1] функция  удовлетворяющая условиям
удовлетворяющая условиям  Эта задача решалась в различных подклассах класса функций, регулярных в круге
Эта задача решалась в различных подклассах класса функций, регулярных в круге 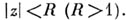 Полученные в нек-ром смысле точные условия выражены в терминах различных ограничений, наложенных на коэффициенты avk разложений
Полученные в нек-ром смысле точные условия выражены в терминах различных ограничений, наложенных на коэффициенты avk разложений
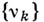 (см. [3]). Эта задача была обобщена, для решения ее были использованы методы теории бесконечных систем линейных уравнений (см. [4]). В частном случае, когда последовательность
(см. [3]). Эта задача была обобщена, для решения ее были использованы методы теории бесконечных систем линейных уравнений (см. [4]). В частном случае, когда последовательность  образует арифметич. прогрессию для целых функций экспоненциального типа, задача о двух точках в известном смысле решена до конца (см. [8]).
образует арифметич. прогрессию для целых функций экспоненциального типа, задача о двух точках в известном смысле решена до конца (см. [8]).