"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ДРОБЬ
Значение ДРОБЬ в математической энциклопедии:
арифметическая - число, состоящее из одной или из нескольких равных частей (долей) единицы. Д. изображается символом  (или a/b), где аи b - целые числа. Числитель аД.
(или a/b), где аи b - целые числа. Числитель аД.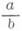 показывает число взятых долей единицы, разделенной на столько долей, какова величина знаменателя b. Д. можно рассматривать также, как частное от деления ана b.
показывает число взятых долей единицы, разделенной на столько долей, какова величина знаменателя b. Д. можно рассматривать также, как частное от деления ана b.
Д. не меняется, если ее числитель и знаменатель умножить на одно и то же отличное от нуля целое число. Благодаря этому любые две Д.
не меняется, если ее числитель и знаменатель умножить на одно и то же отличное от нуля целое число. Благодаря этому любые две Д.  и
и  можно привести к общему знаменателю, т. е. заменить
можно привести к общему знаменателю, т. е. заменить 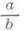 и
и  на равные им Д., имеющие один и тот же знаменатель. Кроме того, Д. можно сокращать, поделив ее числитель и знаменатель на одно и то же число, вследствие чего, всякую Д. можно представить в виде несократимой, т. е. такой, у к-рой числитель и знаменатель не имеют общих множителей.
на равные им Д., имеющие один и тот же знаменатель. Кроме того, Д. можно сокращать, поделив ее числитель и знаменатель на одно и то же число, вследствие чего, всякую Д. можно представить в виде несократимой, т. е. такой, у к-рой числитель и знаменатель не имеют общих множителей.
Сумма и разность Д.  и
и  с одинаковыми знаменателями определяются по правилу:
с одинаковыми знаменателями определяются по правилу:

Чтобы сложить или вычесть Д. с разными знаменателями, надо предварительно привести их к общему знаменателю. Обычно в качестве общего знаменателя дробей  и
и  берется наименьшее общее кратное чисел bи d. Умножение и деление Д. производятся по правилам:
берется наименьшее общее кратное чисел bи d. Умножение и деление Д. производятся по правилам:
Д.  наз. правильной, если ее числитель меньше знаменателя, инеправильной - в противном случае. Д. наз. десятичной, если ее знаменатель является степенью числа 10 (см. Десятичная дробь).
наз. правильной, если ее числитель меньше знаменателя, инеправильной - в противном случае. Д. наз. десятичной, если ее знаменатель является степенью числа 10 (см. Десятичная дробь).
Формальное определение дробей. Д. могут быть определены как упорядоченные пары целых чисел ( а, b), где  для к-рых задано отношение эквивалентности (отношение равенства Д.), а именно, считается, что ( а, b)= ( с, d), если ad=bc. Кроме того, во множестве Д. определены операции сложения, вычитания, умножения и деления, подчиненные следующим правилам:
для к-рых задано отношение эквивалентности (отношение равенства Д.), а именно, считается, что ( а, b)= ( с, d), если ad=bc. Кроме того, во множестве Д. определены операции сложения, вычитания, умножения и деления, подчиненные следующим правилам:

(таким образом, деление определено только в том случае, когда  ).
).
Подобное определение Д. удобно для обобщений и принято в современной алгебре (см. Частных кольцо).
С. А. Степанов.

 (или a/b), где аи b - целые числа. Числитель аД.
(или a/b), где аи b - целые числа. Числитель аД.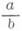 показывает число взятых долей единицы, разделенной на столько долей, какова величина знаменателя b. Д. можно рассматривать также, как частное от деления ана b.
показывает число взятых долей единицы, разделенной на столько долей, какова величина знаменателя b. Д. можно рассматривать также, как частное от деления ана b. не меняется, если ее числитель и знаменатель умножить на одно и то же отличное от нуля целое число. Благодаря этому любые две Д.
не меняется, если ее числитель и знаменатель умножить на одно и то же отличное от нуля целое число. Благодаря этому любые две Д.  и
и  можно привести к общему знаменателю, т. е. заменить
можно привести к общему знаменателю, т. е. заменить 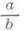 и
и  на равные им Д., имеющие один и тот же знаменатель. Кроме того, Д. можно сокращать, поделив ее числитель и знаменатель на одно и то же число, вследствие чего, всякую Д. можно представить в виде несократимой, т. е. такой, у к-рой числитель и знаменатель не имеют общих множителей.
на равные им Д., имеющие один и тот же знаменатель. Кроме того, Д. можно сокращать, поделив ее числитель и знаменатель на одно и то же число, вследствие чего, всякую Д. можно представить в виде несократимой, т. е. такой, у к-рой числитель и знаменатель не имеют общих множителей. и
и  с одинаковыми знаменателями определяются по правилу:
с одинаковыми знаменателями определяются по правилу:
 и
и  берется наименьшее общее кратное чисел bи d. Умножение и деление Д. производятся по правилам:
берется наименьшее общее кратное чисел bи d. Умножение и деление Д. производятся по правилам:
 наз. правильной, если ее числитель меньше знаменателя, инеправильной - в противном случае. Д. наз. десятичной, если ее знаменатель является степенью числа 10 (см. Десятичная дробь).
наз. правильной, если ее числитель меньше знаменателя, инеправильной - в противном случае. Д. наз. десятичной, если ее знаменатель является степенью числа 10 (см. Десятичная дробь). для к-рых задано отношение эквивалентности (отношение равенства Д.), а именно, считается, что ( а, b)= ( с, d), если ad=bc. Кроме того, во множестве Д. определены операции сложения, вычитания, умножения и деления, подчиненные следующим правилам:
для к-рых задано отношение эквивалентности (отношение равенства Д.), а именно, считается, что ( а, b)= ( с, d), если ad=bc. Кроме того, во множестве Д. определены операции сложения, вычитания, умножения и деления, подчиненные следующим правилам:
 ).
).