" 0 C F G H K L N P S T W Z А Б В Г Д Е Ж З И Й К Л М Н О П Р С Т У Ф Х Ц Ч Ш Э Ю Я

ДОПОЛНИТЕЛЬНАЯ СЕРИЯ

Значение ДОПОЛНИТЕЛЬНАЯ СЕРИЯ в математической энциклопедии:

представлений- семейство неприводимых непрерывных унитарных представлений локально компактной группы G, ненулевые матричные элементы к-рых не могут быть аппроксимированы конечными линейными комбинациями матричных элементов регулярного представления группы Gв топологии равномерной сходимости на компактах в G. Д. с. группы Gнепуста в том и только в том случае, если Gне аменабельна, т. е. если на пространстве 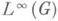не существует нетривиального левоинвариантного среднего (см. [2]). Связная группа Ли Gтогда и только тогда имеет непустую Д. с, когда полупростая факторгруппа группы Gпо максимальному связному разрешимому нормальному делителю группы Gнекомпактна (см. Леви- Мальцева разложение). Д. с. впервые обнаружена для комплексных классич. групп [1]. Д. с. полностью описана (к 1978) лишь для нек-рых локально компактных групп. Некрые задачи теории чисел (см., напр., [5]) равносильны задачам теории представлений, связанных с Д. с. групп аделей линейных алгебраич. групп.

Лит.:[1] Гельфанд И. М., Наймарк М. А., Унитарные представления классических групп, М., 1950; [2] Гринлиф Ф., Инвариантные средние на топологических группах и их приложения, пер. с англ., М., 1973; [3] Наймарк М. А., Линейные представления группы Лоренца, М., 1958; [4] Костант Б., "Математика", 1970, т. 14, № 2, с. 102-16; [5] Petersson H., "Math. Ann.", 1937/1938, Bd 115, S. 23 - 67.

А. И. Штерн.