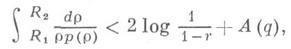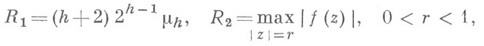|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ДЛИНЫ И ПЛОЩАДИ ПРИНЦИПЗначение ДЛИНЫ И ПЛОЩАДИ ПРИНЦИП в математической энциклопедии: - принцип, выражающий зависимость между длинами кривых, принадлежащих нек-рому специальному семейству, и площадью, покрываемой этим семейством кривых. Пусть w=f(z)- регулярная в открытом множестве Gфункция. Пусть n(w)- число корней уравнения f(z)=w, лежащих в G; l(r)- суммарная длина кривых в G, на к-рых |f(z)|=p; А-площадь Gи
тогда Д. и п. п. выражается неравенством (см. [2]):
Д. и п. п. получил широкое применение в теории функций комплексного переменного (см. [1] - [4]). Д. и п. п. используется, напр., при изучении свойств функций, регулярных в круге |z|<l. В частности, с помощью Д. и п. п. доказывается следующая теорема (см. [2]): если функция w=f(z)=a0+a1z+ ...,mq=max |av|, регулярна в |z|<1 и имеет в нем не более
где
(д)- константа, зависящая от д. Д. и п. п. и различные его обобщения (напр., длины и объема принцип) применяются и в случае га-мерных пространств к квазиконформным отображениям, а также к отображениям с ограниченным Дирихле интегралом (см. [4] - [7]). При выводе Д. и п. п. существенным образом используется неравенство Буняковского. Дальнейшее рассмотрение связи между длинами кривых и площадью, покрываемой ими, привело к важному методу изучения однолистных конформных и квазиконформных отображений - экстремальной метрики методу (см., напр., [8]). В конце 20-х - начале 30-х гг. метод экстремальной метрики в менее совершенной форме (метод полос) успешно применялся для исследования свойств указанных выше отображений односвязных и многосвязных областей. Лит.:[1] Ahlfors L. W., "Acta Soc. scient. fennica", 1930, A. 1, №9; [2] Xeйман В. К., Многолистные функции, пер. с англ., М., 1960; [3] Неванлинна Р., Однозначные аналитические функции, пер. с нем., М,-Л., 1941; [4] Суворов Г. Д., Семейства плоских топологических отображений, Новосиб., 1965; [5] Крейнес М. А., "Матем. сб.", 1941, т. 9, № 3, с. 713-19; [6] Овчинников И. С, "Метрические вопросы теории функций и отображений", 1971, в. <З, с. 98-115; [7] Lе1оng-Ferrand J., Representation conforme et transformations a integral de Dirichlet bornees, P., 1955; [8] Дженкинс Дж ., Однолистные функции и конформные отображения, пер. с англ., М., 1962. И. П. Митюк. |
|
|
|

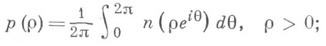
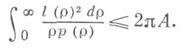
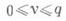 qнулей, из которых не более h лежит в |z|<1/2, то
qнулей, из которых не более h лежит в |z|<1/2, то