|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ДИФФЕРЕНЦИРУЕМЫЙ ВЕКТОРЗначение ДИФФЕРЕНЦИРУЕМЫЙ ВЕКТОР в математической энциклопедии: в пространстве Vпредставления Тгруппы Ли G- вектор
является бесконечно дифференцируемой (класса С 00) вектор-функцией на Gсо значениями в V. Для дифференцируемости вектор-функции f : Наличие дифференцируемых векторов в пространстве представления группы Ли позволяет построить представление соответствующей алгебры Ли и тем самым связать теорию представлений групп Ли с теорией представлений алгебр Ли (см. [6] § 10). Лит.:[1] Grothendieck A., Espaces vectoriels topolofiques, Sao Paulo, 1954; [2] Гельфанд И. М., "Докл. АН СССР", 1939, т. 25, с. 711 - 16; [3] Garding L., "Proc. Nat. Acad. Sci. USA", 1947, v. 33, p. 331-32; [4] Mооrе R. Т., Measurable, continuos and smooth vectors for semigroups and group representations, Providence, 1968; [5] Желобенко Д. П., "Вестн. МГУ. Сер. матем.", 1965, т. 1, с. 3-10; [6] Кириллов А. А., Элементы теории представлений, 2 изд., М., 1978. А. А. Кириллов. |
|
|
|

 для к-рого отображение
для к-рого отображение
 необходимо (а в случае локально выпуклого квазиполного пространства Vи достаточно), чтобы были дифференцируемы все скалярные функции вида
необходимо (а в случае локально выпуклого квазиполного пространства Vи достаточно), чтобы были дифференцируемы все скалярные функции вида  где F- линейный непрерывный функционал на V(см. [1]). Теорема Гельфанда - Гординга: если Т- непрерывное представление группы Ли Gв банаховом пространстве V, то множество
где F- линейный непрерывный функционал на V(см. [1]). Теорема Гельфанда - Гординга: если Т- непрерывное представление группы Ли Gв банаховом пространстве V, то множество 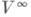 дифференцируемых векторов плотно в V. Для однопараметрич. групп эта теорема доказана в [2], на общий случай доказательство перенесено в [3]. Обобщение этого результата на широкий класс представлений в локально выпуклых пространствах получено в [4], см. также [5].
дифференцируемых векторов плотно в V. Для однопараметрич. групп эта теорема доказана в [2], на общий случай доказательство перенесено в [3]. Обобщение этого результата на широкий класс представлений в локально выпуклых пространствах получено в [4], см. также [5].