Математический словарь
|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ДИФФЕРЕНЦИРОВАНИЕ В СИЛУ СИСТЕМЫЗначение ДИФФЕРЕНЦИРОВАНИЕ В СИЛУ СИСТЕМЫ в математической энциклопедии: - оператор, к-рый определяется следующим образом. Пусть
-автономная система,
где x(t, х 0)- решение системы (*) такое) что x(t0, х 0)=х 0. Свойства оператора qf:1) линейность по j, 2) qf(j1j2)=j1qfj2+j2qfj1. Функция (qfj)(x)совпадает с производной j по векторному полю f. Лит.:[1] Понтрягин Л. С, Обыкновенные дифференциальные уравнения, 3 изд., М., 1970. М. В. Федорюк |
|
|
|


 f=(f1, ... ,fn) и fj : G
f=(f1, ... ,fn) и fj : G R - гладкие отображения, где G- область в Rn. Пусть дано гладкое отображение j :
R - гладкие отображения, где G- область в Rn. Пусть дано гладкое отображение j :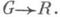 Производная qfj в силу системы (*) функции j в точке
Производная qfj в силу системы (*) функции j в точке 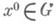 определяется выражением
определяется выражением