|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ С МАЛЫМ ПАРАМЕТРОМ ПРИ ПРОИЗВОДНЫХЗначение ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ С МАЛЫМ ПАРАМЕТРОМ ПРИ ПРОИЗВОДНЫХ в математической энциклопедии: - система вида
где z и у суть, соответственно, М- и m-мерные векторы, m>0 - малый параметр. Полагая в (1) формально m=0, получим так наз. вырожденную систему
Пусть решение x(t,m) системы (1) (хозначает z и ув совокупности) определяется нек-рыми дополнительными условиями. При выяснении возможности использования уравнений (2) для построения асимптотического при малых m приближения к x(t,m) возникают трудности, связанные с тем, что система (2) более низкого порядка, чем (1), и поэтому ее решение не может удовлетворить всем условиям, поставленным для (1). Априори не ясно, какие из дополнительных условий, поставленных для (1), следует оставить для определения решения (2), а какие - отбросить. Кроме того, уравнение F(z, у,t) = 0 имеет относительно z, вообще говоря, несколько корней, и снова априори не ясно, какой из этих корней нужно выбрать при решении системы (2), чтобы получить правильное приближение. Эти моменты отличают постановку задачи об асимптотике решения системы (1) от регулярного случая, когда mвходит не в качестве множителя при производных, а в правые части и притом регулярно. Первые работы, относящиеся к системе вида (1), были посвящены начальной задаче
В наиболее законченной форме результат был дан А. Н. Тихоновым [1]. В общих чертах он состоит в следующем. Пусть уравнение F(z, у, t)=0 определяет в нек-рой замкнутой ограниченной области Dнесколько изолированных корней
Введем так называемую присоединенную систему
в к-рой у* и t* рассматриваются как параметры. Возьмем один из корней я=ji и обозначим его z=j(y, t). Корень z=j(y, t)наз. устойчивым в D, если для каждой точки
где yo(t)находится из системы
при начальном условии y0|t=0=y0; T связано с размерами области D. Таким образом, в отличие от регулярного случая близость при малых m решения x(t,m)системы (1) к решению системы, в к-рой положено m=0, т. е. системы (2), имеет место только при специальных условиях. Предельный переход (6) не является равномерным в связи с тем, что, вообще говоря, Понятие устойчивости корня z=j(y, t )играет большую роль при исследовании системы (1). Различным критериям устойчивости точки покоя по Ляпунову (см. Устойчивость по Ляпунову )соответствуют различные критерии устойчивости корня z=j(y, t). Наиболее употребителен критерий первого приближения, состоящий в требовании, чтобы собственные значения Xматрицы
удовлетворяли неравенству Re l<0 в D. Если Re l>0, то для задачи (1), (3) имеет место результат, аналогичный описанному выше, но для t<0. Если матрица (8) имеет собственные значения с действительными частями разных знаков, т. е.
то решение начальной задачи (1), (3), вообще говоря, предела при
то для решения x(t,m)задачи (1), (10), (11) при выполнении нек-рых усло'вий (аналогичных требованию принадлежности начальной точки области влияния устойчивого корня в случае начальной задачи) будет справедлив предельный переход (5), (6), где y0(t)определяется по-прежнему системой (7). При этом предельный переход (6) справедлив для 0<t<T, и пограничный слой появляется как в окрестности t=0, так и в окрестности t=T, поскольку при m=0 происходит "потеря" дополнительных условий (10), заданных и при t=0, и при t-T. Случай (9) получил название условно устойчивого случая (см. [2]). После того как был установлен предельный переход (5), (6), исследование задачи (1), (3) развивалось в направлении построения асимптотич. разложения ее решения. В регулярном случае решение начальной задачи представляется степенным рядом по m
к-рый при условии достаточной гладкости правых частей является асимптотич. рядом. В случае (1), благодаря наличию пограничного слоя, асимптотич. разложение решения носит более сложный характер, а именно: к степенному разложению типа (12) следует добавить еще так наз. пограничный ряд
Члены П kx(t/m) наз. пограничными членами. Они играют роль вблизи t=0, а далее быстро убывают по закону. ехр(at/m), где a>0. (Подробное описание алгоритма построения асимптотич. разложения решения задачи (1), (3) дано в [2]; там же доказано, что остаточный член асимптотич. разложения (13) при достаточной гладкости правых частей (1) имеет порядок O(mn+1) равномерно относительно Асимптотич. представление (13) (при наличии устойчивого корня) или аналогичное ему представление с двумя пограничными слоями (при наличии условно устойчивого корня) дает возможность доказать существование и получить асимптотику решения задач с более сложными дополнительными условиями, чем (3) или (10), (11) (см. [2]):
Во всех описанных выше задачах в построении функции, к к-рой при Существует много работ, посвященных отдельным весьма разнообразным задачам, напр., таким, как исследование случаев обращения Re Xв нуль, исследование (1) на бесконечном промежутке, изучение решения начальной задачи с сингулярными по m начальными значениями z, изучение (1) в абстрактной форме и др. (см. обзор [4]). Большое количество исследований посвящено линейным уравнениям типа (1). Для линейных уравнений одной из характерных задач является задача исследования асимптотики собственных значений и собственных функций (см., напр., [5]), построение асимптотики фундаментальной системы решений в целом. Исследование последнего вопроса сильно затрудняется, если в системе имеются так наз. точки поворота (подробный обзор этого рода проблем см. в [4]). Ряд результатов, полученных для дифференциальных уравнений типа (1), был перенесен на интегро-дифференциальные уравнения с малым параметром при производных (см., напр., [6]). Имеется также значительный круг работ, посвященных уравнениям с частными производными, содержащими при старшей производной малый параметр (см., напр., [5], [7]). Совершенно аналогичные асимптотич. закономерности наблюдаются для дифференциально-разностных уравнений в случае малого отклонения аргумента (см. [4]). Дифференциальные уравнения вида (1), а также другие, сходные с ними в отношении асимптотич. поведения решений, получили, в отличие от регулярного случая, название сингулярно возмущенных уравнений. Для исследования сингулярно возмущенных систем с успехом применяется метод усреднения Крылова - Боголюбова, к-рый особенно эффективен при исследовании колебательных процессов и резонансных явлений; был предложен также так наз. метод подъема, или метод регуляризации (см. [8]). Сингулярно возмущенные уравнения встречаются в самых различных областях физики и техники: в теории нелинейных колебаний, гидродинамике, небесной механике, квантовой механике, кинетике и др. Лит.:[1]Тихонов А. Н., "Матем. сб.", 1952, т. 31, № 3, с. 575-86; [2] Васильева А. Б., Бутузов В. Ф., Асимптотические разложения решений сингулярно возмущенных уравнений, М., 1973; [3]Мищенко Е. Ф., Розов Н. X., Дифференциальные уравнения с малым параметром и релаксационные колебания, М., 1975; [4] Бутузов В. Ф., Васильева А. Б., Федорюк М. В., в кн.: Итоги науки. Математический анализ. 1967, М., 1969, с. 5-75; [5] Вишик М. И., Люстерник Л. А., "Успехи матем. наук", 1957, т. 12, в. 5, с. 3-122; 1960, т. 15, в. 3, с. 3-80; [6] Иманалиев М. И., Асимптотические методы в теории сингулярно-возмущенных интегро-дифференциальных систем, Фр., 1972; [7] Треногий В. А., "Успехи матем. наук", 1970, т. 25, в. 4, с. 123 - 56; [8] Ломов С. А., Теория возмущений сингулярных краевых задач, А.-А., 1976. А. Б. <Васильева. |
|
|
|


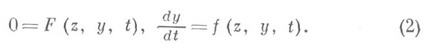
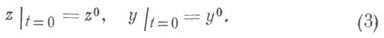
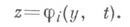

 соответствующая точка покоя z=j(y*, t* )присоединенной системы (4) является асимптотически устойчивой. Областью влияния устойчивого корня z=j(y, t)наз. множество точек (z*, у*, t* )таких, что решение системы (4), определяемое начальным условием z|t=0=z*, стремится к j( у*, t* )при
соответствующая точка покоя z=j(y*, t* )присоединенной системы (4) является асимптотически устойчивой. Областью влияния устойчивого корня z=j(y, t)наз. множество точек (z*, у*, t* )таких, что решение системы (4), определяемое начальным условием z|t=0=z*, стремится к j( у*, t* )при  Оказывается, что если z=j(y, t)- устойчивый корень, а точка (z0, у 0, 0), являющаяся начальной для рассматриваемого решения x(t,m) начальной задачи (3), принадлежит его области влияния, то это решение при m->0 стремится к решению вырожденной системы (2), причем в качестве решения первого уравнения в (2) берется z=j(y, t), а в качестве начального условия - условие (3) для у(условие (3) для zотбрасывается). Другими словами,
Оказывается, что если z=j(y, t)- устойчивый корень, а точка (z0, у 0, 0), являющаяся начальной для рассматриваемого решения x(t,m) начальной задачи (3), принадлежит его области влияния, то это решение при m->0 стремится к решению вырожденной системы (2), причем в качестве решения первого уравнения в (2) берется z=j(y, t), а в качестве начального условия - условие (3) для у(условие (3) для zотбрасывается). Другими словами,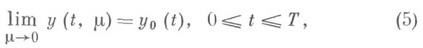
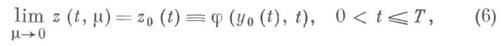
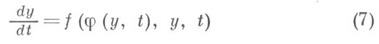
 Иными словами, в связи с "потерей" начальных условий для z, и в окрестности t=0 имеется (правда, бесконечно сужающаяся при
Иными словами, в связи с "потерей" начальных условий для z, и в окрестности t=0 имеется (правда, бесконечно сужающаяся при 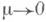 ) область, где z(t,m). и z0(t)не близки. Это явление получило название явления пограничного слоя (название заимствовано из гидродинамики).
) область, где z(t,m). и z0(t)не близки. Это явление получило название явления пограничного слоя (название заимствовано из гидродинамики).

 не имеет. Однако если для (1) поставить не начальную, а краевую задачу, причем при t=0 задать kкомпонент вектора z (компоненты будем обозначать нижними индексами), а при t=T задать М-k компонент вектора z (значение уможно задавать как при t=0, так и при t=T):
не имеет. Однако если для (1) поставить не начальную, а краевую задачу, причем при t=0 задать kкомпонент вектора z (компоненты будем обозначать нижними индексами), а при t=T задать М-k компонент вектора z (значение уможно задавать как при t=0, так и при t=T):


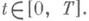 ) Подобного же рода асимптотич. разложение имеет место для решения задачи (1), (10), (11). Отличие заключается в том, что в этом случае к степенному разложению типа (12) добавляются уже два пограничных ряда в связи с наличием пограничного слоя в окрестности и t=0, и t=T.
) Подобного же рода асимптотич. разложение имеет место для решения задачи (1), (10), (11). Отличие заключается в том, что в этом случае к степенному разложению типа (12) добавляются уже два пограничных ряда в связи с наличием пограничного слоя в окрестности и t=0, и t=T.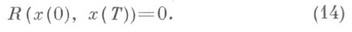
 стремится рассматриваемое решение, участвовал один корень z=j(y, t )уравнения F(z, у, t)=0. Однако при наличии нескольких корней уравнения F(z, у, t)=0 часто наблюдается явление перехода (или срыва), когда решение уравнения (1), удовлетворяющее нек-рым дополнительным (вообще гЬворя, краевым) условиям, имеет в качестве предельной кривую (вообще говоря, разрывную), состоящую из нескольких кусков, каждый из к-рых на соответствующем участке определяется вырожденной системой (2), причем в качестве решения уравнения F(z, у, t) = 0 выбирается надлежащим образом один из корней z=ji(y, t). При переходе от участка к участку корень, вообще говоря, меняется. Границы участков наз. точками срыва. В окрестности каждой точки срыва возникает пограничный слой, называемый внутренним пограничным слоем. Причины срыва весьма разнообразны. В одних случаях асимптотика решения с точками срыва может быть описана разложением типа (13) (см. [2]), в других - носит более сложный характер (см., напр., [3], [4]).
стремится рассматриваемое решение, участвовал один корень z=j(y, t )уравнения F(z, у, t)=0. Однако при наличии нескольких корней уравнения F(z, у, t)=0 часто наблюдается явление перехода (или срыва), когда решение уравнения (1), удовлетворяющее нек-рым дополнительным (вообще гЬворя, краевым) условиям, имеет в качестве предельной кривую (вообще говоря, разрывную), состоящую из нескольких кусков, каждый из к-рых на соответствующем участке определяется вырожденной системой (2), причем в качестве решения уравнения F(z, у, t) = 0 выбирается надлежащим образом один из корней z=ji(y, t). При переходе от участка к участку корень, вообще говоря, меняется. Границы участков наз. точками срыва. В окрестности каждой точки срыва возникает пограничный слой, называемый внутренним пограничным слоем. Причины срыва весьма разнообразны. В одних случаях асимптотика решения с точками срыва может быть описана разложением типа (13) (см. [2]), в других - носит более сложный характер (см., напр., [3], [4]).