|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯЗначение ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ в математической энциклопедии: система бесконечного порядка - бесконечная совокупность дифференциальных уравнений
содержащая бесконечное множество неизвестных функций xk(t), k=1,2, . . ., и их производные. Решением такой системы наз. множество функций {xk(t)}, обращающих все уравнения системы в тождества. Система (1) наз. счетной, в отличие от несчетной системы
где а пробегает нек-рое несчетное множество значений. Система вида (2) содержит в себе несчетное множество функций {xa(t)}, подлежащих определению, и их производные. Рассматриваются также Д. у., содержащие бесконечное множество неизвестных функций двух и более аргументов и их частные производные. Начало развитию теории систем Д. у. вида (1) положила работа А. Н. Тихонова [1]. Основным ее результатом является доказательство теоремы существования решения системы (1) в предположении, что ее правые части определены при произвольных значениях х 1, х 2, . . .(
и о сходимости и равномерной ограниченности рядов
доказана теорема единственности решения xi(t), i=1, 2, . . ., системы (1) при заданных начальных условиях такого, что ряд Дальнейшее развитие теория счетных систем получила в направлении исследований условий ограниченности решений (см. [2]), аналитической зависимости от параметра, устойчивости по Ляпунову и других свойств решений (см. [2]). Особенно глубоко изучены линейные и квазилинейные счетные системы дифференциальных уравнений. К изучению систем бесконечного порядка плодотворно применяются операторные методы. Так, например, вместо системы (1) рассматривается операторное уравнение
где x(t)- бесконечномерный вектор нек-рого банахова пространства В, f(t, x)- бесконечномерная вектор-функция со значениями в том же пространстве, производная рассматривается в смысле Фреше. В частности, для уравнения (3) были получены следующие результаты (см. [3]). Если f(t, x)- ограниченный оператор, то из Выполнения локальной теоремы существования и отрицательности генерального показателя (см. [3]) следует неограниченная продолжимость решений с достаточно близкими к нулю начальными значениями. Если
где е Аt- операторная экспонента. Если где Аимеет прежнее значение, a f(t)- непрерывная T-периодическая вектор-функция, то существует единственное периодическое решение, когда спектр s(А)оператора Ане содержит точек мнимой оси 2kpi/Т, k=0,
найдены условия устойчивости по Ляпунову в нуле в виде требования
при достаточно малом q>0 и расположении спектра оператора Ав левой открытой полуплоскости. Лит.:[1] Тихонов А. Н., "Матем. сб.", 1934, т. 41, в. 4, с. 551-60; [2] Валеев К. Г., Жаутыков О. А., Бесконечные системы дифференциальных уравнений, А.-А., 1974; [3] Далецкий Ю. Л., Крейн М. Г., Устойчивость решений дифференциальных уравнений в банаховом пространстве, М., 1970. И. П. Макаров. |
|
|
|


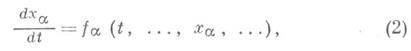
 ), непрерывны по отношению к x1, х 2,... при фиксированном значении t, измеримы по t при фиксированных х 1, х 2,... и ограничены некоторыми суммируемыми на сегменте [t0, t0+a2]. функциями Mi(t), i=1, 2, ... При дополнительных предположениях о выполнении обобщенных условий Липшица
), непрерывны по отношению к x1, х 2,... при фиксированном значении t, измеримы по t при фиксированных х 1, х 2,... и ограничены некоторыми суммируемыми на сегменте [t0, t0+a2]. функциями Mi(t), i=1, 2, ... При дополнительных предположениях о выполнении обобщенных условий Липшица

 сходится.
сходится.
 (где А- бесконечномерная постоянная матрица) - ограниченный оператор, то в гильбертовом пространстве ограниченность всех решений при
(где А- бесконечномерная постоянная матрица) - ограниченный оператор, то в гильбертовом пространстве ограниченность всех решений при  имеет место тогда и только тогда, когда оператор Аподобен косоэрмитову. В этом же случае найдено явное выражение решения задачи Коши с начальными условиями x(t0)=x0 в виде
имеет место тогда и только тогда, когда оператор Аподобен косоэрмитову. В этом же случае найдено явное выражение решения задачи Коши с начальными условиями x(t0)=x0 в виде

 1,
1,  2, ... Для случая
2, ... Для случая
