|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ ВТОРОГО ПОРЯДКАЗначение ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ ВТОРОГО ПОРЯДКА в математической энциклопедии: - уравнение, к-рое содержит хотя бы одну производную 2-го порядка от неизвестной функции и(х)и не содержит производных более высокого порядка. Напр., линейное уравнение 2-го порядка имеет вид
где точка х-( х 1, х 2, ..., х п )принадлежит нек-рой области
где коэффициенты a*ij(x) в точке x0=x(x0) равны нулю при Число кположительных и число lотрицательных в точке x0 коэффициентов В случае двух независимых переменных (n=2) тип уравнения удобнее определять с помощью функции
Так, уравнение (1) является эллиптическим в точке х 0, если D(x0)>0; гиперболическим, если D(х 0)<0, и параболическим в широком смысле, если D(х 0) = 0. Уравнение наз. эллиптическим, гиперболическим и т. д. в области, если оно эллиптично, соответственно, гиперболично и т. д. в каждой точке этой области. Так, напр., уравнение Трикоми уи хх+и уy=О эллиптично при у>0, гиперболично при у<0 и параболично в широком смысле при у=0. Преобразование переменных x0=x(x), к-рое приводит уравнение (1) к канонич. виду в точке х 0, зависит от этой точки. В случае трех и более независимых переменных, вообще говоря, не существует неособого преобразования, приводящего уравнение (1) к канонич. виду одновременно во всех точках нек-рой окрестности точки x0, т. е. к виду
В случае же двух независимых переменных (n=2) такое приведение уравнения (1) к канонич. виду возможно при нек-рых условиях на коэффициенты aij(x);напр., если функции а ij (х) непрерывно дифференцируемы до 2-го порядка включительно и уравнение (1) одного типа в нек-рой окрестности точки х 0. Пусть
- нелинейное уравнение 2-го порядка, где
Для классификации нелинейных уравнений вида (3) фиксируют некоторое решение
с коэффициентами
Уравнение (3) для данного решения К решению дифференциальных уравнений 2-го порядка сводится весьма широкий класс физических задач. См., напр., Волновое уравнение, Телеграфное уравнение, Теплопроводности уравнение, Лапласа уравнение, Пуассона уравнение, Гельмгольца уравнение, Трикоми уравнение А. К. Гущин. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ ПЕРВОГО ПОРЯДКА - уравнение, связывающее искомую функцию и(х), ее первые производные Diu=uxi, i=1,..., п, и независимые переменные x= ( х г, . . ., х п). Всякая система дифференциальных уравнений с частными производными может быть приведена к нек-рой системе Д. у. с ч. <п. <п. <п. Для этого достаточно ввести в качестве новых искомых функций все частные производные от каждой функции ui(x)до порядка li-1 включительно, если хотя бы одна производная порядка li входит в к.-л. уравнение рассматриваемой системы. При этом систему следует пополнить новыми уравнениями, выражающими равенство различных смешанных производных. Напр., уравнение
после введения вспомогательных искомых функций v=ux, w=uy приводится к следующей системе уравнений 1-го порядка:
(последние три уравнения не независимы). Одно Д. у. с ч. п. п. п. с одной искомой функцией задается соотношением:
где р=( р 1, р 2, ..., р п)=(D1u, D2u,..., Dnu). Всякое решение и=и (х)уравнения (1) при определенных требованиях определяет нек-рую поверхность (интегральную поверхность) в пространстве Е п+1 переменных ( х 1, . .., х п, и), причем р;являются компонентами вектора нормали к этой поверхности. Поэтому уравнение (1) задает связь между составляющими pi вектора нормали к интегральной поверхности и в каждой точке ( х, и )определяет (n-1)-параметрич. семейство касательных к интегральной поверхности плоскостей [или несколько таких семейств, соответствующих различным решениям уравнения (1) относительно р]. Огибающая этого семейства плоскостей наз. конусом Монжа [в данной точке ( х, u)], а направления его образующих - характеристическими направлениями. В каждой точке ( х, и )эти направления определяются уравнениями
где р=(p1, р 2, . .., р п)- любой вектор, удовлетворяющий уравнению (1). Кривая с непрерывно изменяющейся касательной, имеющая в каждой своей точке характеристич. направление, наз. кривой Монжа, или фокальной кривой. Фокальная кривая является интегральной кривой системы (2) при произвольно заданном непрерывно дифференцируемом векторе р=р( х, и )таком, что F[x, и, р) = 0. Поскольку каждой точке фокальной кривой сопоставлен вектор р, определяющий направление плоскости, касательной к кривой в этой точке, то фокальная кривая задается одновременно со своими касательными плоскостями и наз. поэтому фокальной полосой. Если s - параметр на фокальной кривой, то уравнение Если фокальная кривая принадлежит интегральной поверхности и=и (х)уравнения (1) и в каждой ее точке выполнены равенства р i=Diu (х), то она наз. характеристической кривой (бихарактеристикой),а соответствующая фокальная полоса - характеристической полосой. Характеристич. полоса определяется системой уравнений:
к-рая наз. характеристической системой уравнения (1). Функция F(x, и, р )является интегралом системы уравнений (3), поэтому условие F=0 выполнено на всей характеристич. кривой, если оно выполнено в к.-л. ее точке. Интегральная поверхность уравнения (1), касаясь в каждой своей точке конуса Монжа, является огибающей семейства конусов Монжа и тем самым - огибающей семейства характеристич. полос. Последнее означает, что интегральная поверхность состоит из характеристич. кривых, так что ее нахождение сводится к интегрированию характеристич. системы (3). Фокальные кривые, не сводящиеся к характеристическим (если они существуют), являются огибающими последних на интегральной поверхности u=u(х). Их проекции на пространство ( х 1, х 2,.. ., х n )состоят из точек сингулярности решения и(х). Уравнение (1) наз. квазилинейным, если
Уравнения (2) в этом случае имеют вид:
и не содержат р;конус Монжа вырождается в прямую (ось Монжа), и все фокальные кривые являются характеристическими. Задача Коши для уравнения (1) состоит в нахождении интегральной поверхности, проходящей через заданное (п-1)-мерное (начальное) многообразие:
Эта интегральная поверхность состоит из характеристич. кривых, проведенных через точки начального многообразия. В случае квазилинейного уравнения последние получаются интегрированием характеристич. системы (4) с начальными условиями (5). В общем случае для построения характеристич. кривых условия (5) нужно дополнить заданием начальных значений
получающихся дифференцированием условий (5), и уравнения
Ввиду нелинейности, уравнения (6) и (7) определяют р? (Х)и, соответственно, решение задачи Коши (1), (5), вообще говоря, неоднозначно. Пусть
- уравнения характеристич. кривых, проходящих через точки начального многообразия. Если начальное многообразие (5) не является характеристическим (см. Характеристическое многообразие), то эти уравнения - параметрические уравнения искомой интегральной поверхности, они определяют решение и=и (х)задачи Коши, если эта поверхность однозначно проектируется на пространство независимых переменных ( х 1, ..., х п). В случаях, когда уравнения (8) определяют поверхность, не представимую, однако, уравнением и=и (х), т. е. не проектирующуюся однозначно на пространство (x1, ..., х п), вводят понятие обобщенного решения задачи Коши (1), (5). Решение нелинейного уравнения (1), по существу, сводится к решению системы квазилинейных уравнений с одинаковой главной частью:
получающейся дифференцированием уравнения (1). Примеры. (D1u)2+(D2u)2=1; характеристич. полосы задаются уравнениями:
Полным интегралом уравнения (1) наз. решение
уравнения (1), существенно зависящее от ппараметров a1, a2, . .., an. Решение вида (9) есть полный интеграл, если ранг матрицы
равен п(в нек-рой области изменения переменных). Путем образования огибающих из полного интеграла строятся решения уравнения (1), зависящие от произвольных функций. Если из n-параметрич. семейства поверхностей (9) выделить (n-k)-параметрич. семейство, предполагая параметры асвязанными ксоотношениями wi (а) = 0, i=1, 2, ..., k, то огибающая этого семейства зависит от kпроизвольных функций п-kпеременных; соответствующие решения, зависящие от произвольных функций, наз. общими интегралами. Огибающая n-параметрич. семейства (9) (если она существует) не содержит никакого произвола и дает особый интеграл, к-рый может быть также найден исключением риз соотношений F=Fp=0. Многообразие касания поверхности семейства (9) с огибающей этого семейства является характеристич. многообразием кизмерений. В частности, при k=1 это многообразие является характеристич. кривой. На этом основан способ построения общего решения характеристич. системы уравнений (3) по полному интегралу уравнения (1) (метод Якоби), часто применяемый при интегрировании канонич. уравнений. Переопределенные системы Д. у. с ч. п. п. п.- это системы уравнений вида (1), в к-рых число независимых уравнений больше числа искомых функций. Такие системы, вообще говоря, противоречивы, и выделение классов непротиворечивых (совместных) систем составляет предмет теории совместности дифференциальных уравнений с частными производными. Пусть имеется переопределенная система
для одной искомой функции и(х). Пусть все уравнения системы (10) независимы, так что
({ , } - скобки Пуассона) являются следствиями исходных уравнений, и незамкнутой - в противном случае. Незамкнутую систему с помощью присоединения независимых уравнений вида (11) можно расширить до замкнутой. При т= п замкнутая система имеет только тривиальное решение, а при т<п количество ее независимых решений равно п- т. Лит.:[1] Goursat E., Lecons sur l'integration des equations aux derivees partielles du premier ordre, 2 ed., P., 1921; [2] Caratheоdоrу С, Variationsrechnung und partielle Differentialgleichungen erster Ordnung, Lpz.- В., 1935; [3] Гюнтер Н. <М., Интегрирование уравнений первого порядка в частных производных, Л.- М., 1934; [4] Курант Р., Уравнения с частными производными, пер. с англ., М., 1964; [5] Петровский И. Г., Лекции по теории обыкновенных дифференциальных уравнений, 6 изд., М., 1970; [6] его же, Лекции об уравнениях с частными производными, 3 изд., М., 1961; [7] Картан Э., Внешние дифференциальные системы и их геометрические приложения, пер. с франц., 1962; [8] Рашевский П. К., Геометрическая теория уравнений с частными производными, М.- Л., 1947; [9] Фиников С. II., Метод внешних форм Картана в дифференциальной геометрии, М.- Л., 1948; [10] Яненко Н. Н., Рождественский Б. Л., Системы квазилинейных уравнений и их приложения к газовой динамике, М., 1968. Я. Я. Кузнецов, Б. Л. Рождественский. ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ЧАСТНЫМИ ПРОИЗВОДНЫМИ С ОСОБЕННОСТЯМИ В КОЭФФИЦИЕНТАХ - уравнение с частными производными, коэффициенты и свободный член к-рого на некоторых многообразиях из замыкания области их задания имеют разрывы первого рода или обращаются в бесконечность. Типичными уравнениями такого типа являются, например, уравнение Лаврентьева - Бицадзе
или
где D - оператор Лапласа по переменным х 1, . .., х п. К уравнениям с особенностями в коэффициентах относятся многие вырожденные уравнения с частными производными. Центральное место в теории дифференциальных уравнений с особенностями в коэффициентах занимает исследование разрешимости начальных краевых и смешанных задач в их классической и обобщенной постановках, а также поиск новых корректно поставленных задач. Сравнительно полно исследованы краевые задачи для линейных эллиптич., гиперболич. и параболич. уравнений 2-го порядка со слабыми особенностями в коэффициентах, к-рые, как правило, суммируемы со, степенью, большей размерности области их задания. В случае, когда коэффициенты этих уравнений претерпевают лишь разрывы первого рода на нек-рых достаточно гладких поверхностях, лежащих внутри области задания, создана весьма полная теория основных краевых задач. См. Дифференциальное уравнение с частными производными;задача с разрывными коэффициентами, а также [3], [5], [6]. Лит.:[1] Бицадзе А. В., Уравнения смешанного типа, М., 1959; [2] Векуа И. Н., Обобщенные аналитические функции, М., 1959; [3] Ладыженская О. А., Уральцева Н. Н., Линейные и квазилинейные уравнения эллиптического типа, М., 1964; [4] Миранда К., Уравнения с частными производными эллиптического типа, пер. с итал., М., 1957; [5] Олейник О. А., "Докл. АН СССР", 1959, т. 124, № 6, с. 1219 - 22; [6] Самарский А. А., "Докл. АН СССР", 1958, т. 121, №2, с. 225 - 28. А. М. Нахушев. |
|
|
|

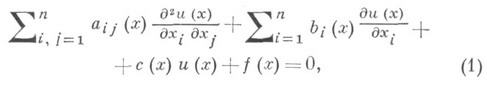
 в к-рой определены действительнозначные функции aij(x), bi (х), с (х), и в каждой точке
в к-рой определены действительнозначные функции aij(x), bi (х), с (х), и в каждой точке  хотя бы один из коэффициентов aij(x)обличен от нуля. Для любой точки
хотя бы один из коэффициентов aij(x)обличен от нуля. Для любой точки  существует такое неособое преобразование независимых переменных x=x(x), что уравнение (1) в новых координатах x= (x1, x2, ...,xn). примет вид
существует такое неособое преобразование независимых переменных x=x(x), что уравнение (1) в новых координатах x= (x1, x2, ...,xn). примет вид
 и равныили
и равныили  О при i= j. Уравнение (2) наз. канонич. видом уравнения (1) в точке х 0.
О при i= j. Уравнение (2) наз. канонич. видом уравнения (1) в точке х 0. в уравнении (2) зависит только от коэффициентов aij(x)уравнения (1). Это обстоятельство позволяет классифицировать дифференциальные уравнения (1) следующим образом. Если k=n или l=п, то уравнение (1) наа. эллиптическим в точке х 0;. если k=п-1, а l= 1, или k=1, а l=п-1, то - гиперболическим; если k+l=п и 1<k<n-1, то - ультрагиперболическим. Уравнение наз. параболическим в широком смысле в точке х 0, если хотя бы один из коэффициентов
в уравнении (2) зависит только от коэффициентов aij(x)уравнения (1). Это обстоятельство позволяет классифицировать дифференциальные уравнения (1) следующим образом. Если k=n или l=п, то уравнение (1) наа. эллиптическим в точке х 0;. если k=п-1, а l= 1, или k=1, а l=п-1, то - гиперболическим; если k+l=п и 1<k<n-1, то - ультрагиперболическим. Уравнение наз. параболическим в широком смысле в точке х 0, если хотя бы один из коэффициентов  равен нулю в точке x0=x(x0), k+l<n; уравнение наз. параболическим в точке х 0, если только один из коэффициентов
равен нулю в точке x0=x(x0), k+l<n; уравнение наз. параболическим в точке х 0, если только один из коэффициентов  равен нулю в точке x0 (пусть
равен нулю в точке x0 (пусть  ), а все остальные коэффициенты
), а все остальные коэффициенты  одного знака и коэффициент
одного знака и коэффициент 




 и пусть в каждой точке из области определения действительнозначной функции Ф существуют производные
и пусть в каждой точке из области определения действительнозначной функции Ф существуют производные  и выполнено условие
и выполнено условие
 этого уравнения и рассматривают линейное уравнение
этого уравнения и рассматривают линейное уравнение

 наз. эллиптическим, гиперболическим и т. д. в точке х 0 (или в области), если эллиптично, гиперболично и т. д. в этой точке (соответственно в области) уравнение (4).
наз. эллиптическим, гиперболическим и т. д. в точке х 0 (или в области), если эллиптично, гиперболично и т. д. в этой точке (соответственно в области) уравнение (4).

 (1)
(1)
 системы (2) наз. уравнением (или условием) полосы.
системы (2) наз. уравнением (или условием) полосы.



 к-рые определяются из уравнений:
к-рые определяются из уравнений:




 характеристич. система (3) имеет вид
характеристич. система (3) имеет вид  уравнения характеристик:
уравнения характеристик: и=u0, решение задачи Коши с начальным условием и( х, 0)=и 0 (х)задается параметрич. уравнениями
и=u0, решение задачи Коши с начальным условием и( х, 0)=и 0 (х)задается параметрич. уравнениями



 Эта система наз. замкнутой, если все уравнения вида
Эта система наз. замкнутой, если все уравнения вида
 и уравнение Эйлера - Пуассона-Дарбу
и уравнение Эйлера - Пуассона-Дарбу
