|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ОТКЛОНЯЮЩИМСЯ АРГУМЕНТОМЗначение ДИФФЕРЕНЦИАЛЬНОЕ УРАВНЕНИЕ С ОТКЛОНЯЮЩИМСЯ АРГУМЕНТОМ в математической энциклопедии: - дифференциальное уравнение, связывающее аргумент, искомую функцию и ее производные, взятые, вообще говоря, при различных значениях этого аргумента. Примеры:
где постоянные а, t, kзаданы; т в уравнении (1) и t-kt в уравнении (2) - отклонения аргумента. Встречаются и более сложные Д. у. с о. а., включающие большее число отклонений аргумента,. могущих представлять собой заданные функции (в частности, если они постоянны, то уравнение часто наз. дифференциально-разностным) или даже зависеть от искомого решения. Эпизодически рассматривались также Д. у. с о. а., в к-рых искомая функция зависит более чем от одного аргумента. Д. у. с о. а. впервые появились в связи с формальным решением уравнений с частными производными и затем неоднократно рассматривались как сами по себе, так и в связи с задачами геометрии, а позднее - в связи с различными приложениями, прежде всего к теории автоматич. управления. Построение систематич. теории Д. у. с о. а. было начато в 1949. Определение Д. у. с о. а. допускает любые суперпозиции искомого решения [типа x(x(t))]и интегралы от него, поэтому формально класс Д. у. с о. а. включает в себя все уравнения математич. анализа. Все же обычно, говоря о Д. у. с о. а., имеют в виду тот или иной естественный класс дифференциальных уравнений, в к-рых введено отклонение аргумента, допускающее построение содержательной теории. При этом ряд свойств Д. у. с о. а. имеет непосредственную аналогию со свойствами обычных дифференциальных уравнений, тогда как иные свойства являются принципиально новыми. Уравнение (или система уравнений)
(для системы хи f - векторы), где все tj>0, наз. уравнением (системой) запаздывающего, нейтрального или опережающего типа, если maxjmj<n, =n,>n, соответственно. Для уравнений иных видов такая классификация проводится на основе преобразования к виду (3) с помощью замены Если отклонения tj зависят от t, то уравнение (3) может менять тип; напр., уравнение (2) для Один из простейших классов Д. у. с о. а. следующий:
Для этого класса Д. у. с о. а. ставится основная начальная задача: заданы начальная точка t0, начальная функция j(t), Аналогично ставится начальная задача и строится решение для систем уравнений вида (4) и для уравнений высших порядков. В случае нескольких запаздываний за шаг принимают наименьшее из них. Если t=t(t), то j(t) должна быть задана на всем начальном множестве значений Решение сформулированной начальной задачи строится только в направлении возрастания t. Другая ее особенность состоит в том, что многообразие решений при произвольной j(t), вообще говоря, бесконечномерное. (Исключением служат уравнения беа предыстории, для к-рых В уравнении (4) запаздывание сосредоточенное. Рассматриваются также уравнения с распределенным запаздыванием, правая часть к-рьм включает интегралы
(это - интегро-дифференциальные уравнения типа Вольтерра) или, комбинированный случай,
и т. п. Наиболее общим видом Д. у. с о. а. запаздывающего типа 1-го порядка служит дифференциально-функциональное уравнение типа Вольтерра
где правая часть при каждом t>t0 представляет coбoй функционал. И для таких уравнений начальная задача разрешима. Для Д. у. с о. а. нейтрального типа, напр.
постановка и свойства начальной задачи аналогичны указанным выше, однако свойство сглаживания отсутствует; кроме того, возможны осложнения, если переменное запаздывание t2(t) имеет нули. Начальная задача для Д. у. с о. а. опережающего типа является некорректной. Лучше других изучены линейные автономные (т. е с постоянными коэффициентами и постоянными отклонениями аргумента) Д. у. с о. а. Уравнение (бе; подобных членов)
(все а j неравны 0) имеет частные решения x=ept, где рудовлетворяет характеристическому уравнению
Здесь Р(р)- квазиполином; k-кратному корню уравнения (6) отвечают решения ept,. .., tk-1ept уравнения (5). Если хотя бы одно
В этих случаях каждое решение уравнения (5) разлагается в ряд по указанным частным решениям, а при решении начальной задачи для уравнения (5) и соответствующего неоднородного уравнения можно пользоваться обычными методами операционного исчисления. Аналогичными свойствами обладают системы уравнений и уравнения с распределенным запаздыванием. Обычные определения устойчивости решения непосредственно распространяются на Д. у. с о. а. запаздывающего и нейтрального типов. Для асимптотич. устойчивости решений уравнения (5) необходимо и достаточно условие:
При выполнении этого условия асимптотически устойчиво и нулевое решение нелинейных автономных уравнений, для к-рых (5) служит линейным приближением. Метод функций Ляпунова на исследование устойчивости Д. у. с о. а. распространил Н. Н. Красовский [5]. Он предложил пользоваться функционалами V[y(s); t]в
Аналог теоремы Ляпунова об устойчивости: если
то тривиальное решение уравнения (4) устойчиво. Основные теоремы об устойчивости, выраженные в таких терминах, допускают обращение. Ряд результатов получен для периодических Д. у. с о. а. Так, если
то неподвижные точки оператора
Из других направлений исследования Д. у. с о. а. выделяются: детальное изучение асимптотических и осцилляционных свойств уравнений
и аналогичных уравнений 2-го порядка; получение асимптотич. выражений для решений систем с малыми отклонениями аргумента или с малой нелинейностью; распространение на Д. у. с о. а. асимптотич. методов Крылова - Боголюбова (см. Крылова- Боголюбова метод усреднения);распространение на Д. у. с о. а. теории оптимального управления Л. С. Понтрягина (см. Оптимального управления математическая теория);исследование краевых задач; исследование эволюционных уравнений с частными производными и запаздыванием во времени; исследование стохастич. Д. у. с о. а. (см. Стохастическое дифференциальное уравнение )и т. д. Лит.:[1] Эльсгольц Л. Э., Норкин С. Б., Введение в теорию дифференциальных уравнений с отклоняющимся аргументом, М., 1971; [2] Пинни Э., Обыкновенные дифференциально-разностные уравнения, пер. сангл., М., 1961; [3] Беллман Р., Кук К. Л., Дифференциально-разностные уравнения, пер. с англ., М., 1967; [4] Мышкис А. Д.. Линейные дифференциальные уравнения с запаздывающим аргументом, 2 изд., М., 1972; [5] Красовский Н. Н., Некоторые задачи теории устойчивости движения, М., 1959; [6] Норкин С. Б., Дифференциальные уравнения второго порядка с запаздывающим аргументом, М., 1965; [7] Рубаник В. П., Колебания квазилинейных систем с запаздыванием, М., 1969; 18] Оguztorеli M. N., Time-Lag control systems, N. Y.- L., 1966; [9] Halanау A., Differential equations, N.Y.- L., 1966; [10] Hale J. K., Functional differential equations, N. Y., 1971. А. Д. Мышкис. |
|
|
|



 c - возрастающая функция; напр., уравнение (1) запаздывающего типа при t>0 и опережающего (замена
c - возрастающая функция; напр., уравнение (1) запаздывающего типа при t>0 и опережающего (замена  ) - при t<0.
) - при t<0. запаздывающего типа при
запаздывающего типа при  и опережающего - при t<0. Если tj зависят от искомого решения, то уравнение (3) может иметь различный тип для различных его решений. Наиболее подробно разработана теория Д. у. с о. а. запаздывающего типа, менее - нейтрального типа и почти не изучена теория уравнений опережающего типа.
и опережающего - при t<0. Если tj зависят от искомого решения, то уравнение (3) может иметь различный тип для различных его решений. Наиболее подробно разработана теория Д. у. с о. а. запаздывающего типа, менее - нейтрального типа и почти не изучена теория уравнений опережающего типа.
 и значение x(t0+0); под решением задачи для уравнения (4) понимается функция x(t), t>t0, обращающая уравнение (4) в тождество, причем' при t>t0,
и значение x(t0+0); под решением задачи для уравнения (4) понимается функция x(t), t>t0, обращающая уравнение (4) в тождество, причем' при t>t0,  в правую часть вместо x(t-t) надо подставлять j(t-t). Для решения поставленной задачи можно применить метод шагов: при
в правую часть вместо x(t-t) надо подставлять j(t-t). Для решения поставленной задачи можно применить метод шагов: при  решают начальную задачу для уравнения (4), в к-ром вместо x(t-t) подставлено j(t-t); при
решают начальную задачу для уравнения (4), в к-ром вместо x(t-t) подставлено j(t-t); при  будет to<t-t
будет to<t-t t0+т, т. е. x(t-t) уже построено, и т. д.; таким образом, на каждом шаге приходится решать задачу Коши для уравнения без отклонения аргумента. Если функции f и j непрерывны и x(t0+0)=j(t0), то решение задачи существует на нек-ром интервале
t0+т, т. е. x(t-t) уже построено, и т. д.; таким образом, на каждом шаге приходится решать задачу Коши для уравнения без отклонения аргумента. Если функции f и j непрерывны и x(t0+0)=j(t0), то решение задачи существует на нек-ром интервале  и может быть продолжено обычным образом, а если функция f(t, х, у )удовлетворяет по хусловию Липшица, то это решение единственно и непрерывно зависит от f, ф, т. Если при этом функция f достаточно гладкая, то х' (t)непрерывна при t>t0, x"(t)непрерывна при t>t0+t и т. д. (свойство сглаживания).
и может быть продолжено обычным образом, а если функция f(t, х, у )удовлетворяет по хусловию Липшица, то это решение единственно и непрерывно зависит от f, ф, т. Если при этом функция f достаточно гладкая, то х' (t)непрерывна при t>t0, x"(t)непрерывна при t>t0+t и т. д. (свойство сглаживания).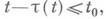 t>t0. Наличие у x(t)нулей препятствует применению метода шагов, однако с помощью простых аппроксимационных или итерационных методов можно доказать теорему о разрешимости начальной задачи, аналогичную приведенной выше. Численные методы ее решения в принципе те же, что для
t>t0. Наличие у x(t)нулей препятствует применению метода шагов, однако с помощью простых аппроксимационных или итерационных методов можно доказать теорему о разрешимости начальной задачи, аналогичную приведенной выше. Численные методы ее решения в принципе те же, что для  Если заданные функции разрывны или
Если заданные функции разрывны или  то понятие решения должно быть естественно обобщено.
то понятие решения должно быть естественно обобщено. при
при  ; напр., уравнение (2) при
; напр., уравнение (2) при  t0=0.) Это существенно отличает теорию Д. у. с о. а. от теории уравнений без отклонения аргумента.
t0=0.) Это существенно отличает теорию Д. у. с о. а. от теории уравнений без отклонения аргумента.





 то уравнение (6) имеет бесконечное число корней р 1, р 2, ... Чтобы уравнение (5) имело запаздывающий (нейтральный) тип, необходимо и достаточно условие
то уравнение (6) имеет бесконечное число корней р 1, р 2, ... Чтобы уравнение (5) имело запаздывающий (нейтральный) тип, необходимо и достаточно условие

 полную производную такого функционала "вдоль решения" заданного уравнения вида (4) можно вычислить в силу этого уравнения, и она представляет собой функционал того же типа, т. е.
полную производную такого функционала "вдоль решения" заданного уравнения вида (4) можно вычислить в силу этого уравнения, и она представляет собой функционал того же типа, т. е.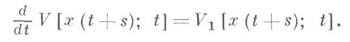



 x(t) - решение уравнения (4) при начальной функции j; k- натуральное) определяют kT-периодич. решения уравнения (4). Этот и другие аналогичные факты дают возможность применить к отысканию периодич. решений и к выяснению их устойчивости методы теории нелинейных операторов. Для линейных однородных Т-периодич. Д. у. с о. а. запаздывающего типа доказана возможность аппроксимации каждого решения с любой степенью точности по шкале экспонент линейной комбинацией решений вида
x(t) - решение уравнения (4) при начальной функции j; k- натуральное) определяют kT-периодич. решения уравнения (4). Этот и другие аналогичные факты дают возможность применить к отысканию периодич. решений и к выяснению их устойчивости методы теории нелинейных операторов. Для линейных однородных Т-периодич. Д. у. с о. а. запаздывающего типа доказана возможность аппроксимации каждого решения с любой степенью точности по шкале экспонент линейной комбинацией решений вида