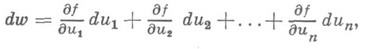|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕЗначение ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ в математической энциклопедии: - раздел математики, в к-ром изучаются понятия производной и дифференциала и способы их применения к исследованию функций. Развитие Д. и. тесно связано с развитием интегрального исчисления. Неразрывно и их содержание. Вместе они составляют основу математич. анализа, имеющего чрезвычайное значение для естествознания и техники. Основной предпосылкой для создания Д. и. явилось введение в математику переменных величин (Р. Декарт, R. Descartes). В общих чертах построение дифференциального и интегрального исчислений было завершено в трудах И. Ньютона (I. Newton) и Г. Лейбница (G. Leibniz) к концу 17 в., однако вопросы обоснования с помощью понятия пре- дела были разработаны О. Коши (A. Couchy) лишь в начале 19 в. Создание дифференциального и интегрального исчисления явилось началом периода бурного развития математики и связанных с ней прикладных наук. Под Д. и. обычно понимают классич. Д. и., в к-ром рассматриваются действительные функции одного или нескольких действительных переменных, хотя в современном толковании может идти речь и о Д. и. в абстрактных пространствах. Д. и. основано на понятиях действительного числа, функции, предела и непрерывности- важнейших понятий математики, сформировавшихся и получивших современное содержание в процессе развития математич. анализа и работы над его обоснованием. Центральные понятия Д. и.- производная и дифференциал- и разработанный в Д. и. аппарат, связанный с ними, доставляют средства для исследований функций, локально сходных . с линейной функцией или многочленом, а именно такие функции в первую очередь интересны для приложений. Производная. Пусть функция y=f(x). определена в нек-рой окрестности точки х 0,
то он наз. производной функции f(x). в точке х 0 и обозначается
Операция вычисления производной наз. дифференцированием. Если f'( х 0)- конечна, функция f(x). наз. дифференцируемой в точке х 0. Функция, дифференцируемая в каждой точке нек-рого промежутка, наз. дифференцируемой в. <промежутке. Геометричес ко е истолкование производной. Пусть С- плоская кривая, заданная в прямоугольной системе координат уравнением y=f(x), где f(х)определена и непрерывна в нек-ром интервале, М( х 0, у 0)- фиксированная точка на С, Р( х, у)- произвольная точка кривой С, МР- секущая (см. рис. 1). Прямая МТ наз. касательной к кривой С в точке М, если угол j между секущей МР и этой прямой стремится к нулю, когда х->х 0 (иными словами, когда точка
Механичес кое истолков а ние производной. Пусть точка Мдвижется прямолинейно по закону s=f(t). За время Dt точка Мсместится на Ds=f(t+Dt)-f(t). Отношение Ds/Dt представляет собой среднюю скорость u ср точки за время Dt. При неравномерном движении ucp не постоянна. Мгновенной скоростью в момент tназ. предел средней скорости при Таким образом, понятие производной доставляет общее решение задачи о построении касательной к плоской кривой и задачи о вычислении скорости прямолинейного движения. Эти две задачи явились основными предпосылками в формировании понятия производной. Функция, имеющая в точке х 0 конечную производную, непрерывна в этой точке. В случае бесконечной производной этого может не быть. Непрерывная функция может не иметь ни конечной, ни бесконечной производной. Существуют непрерывные функции, не имеющие производной ни в одной точке области определения. Для производных основных элементарных функций справедливы следующие формулы (в любой точке области определения; исключения оговариваются):
Имеют место также следующие правила дифференцирования; 1) Если функции и(х)и u(х)дифференцируемы в точке х 0, то функции
также дифференцируемы в этой точке, причем
2) Теорема о производной сложной функции: если функция y=f(u)дифференцируема в точке и 0, а функция j(х)дифференцируема в точке х 0, причем u0=j(xo), то сложная функция y-f(j(x))дифференцируема в точке х 0 и y'x=f(u0)j'(x0) или, в другой записи, 3) Теорема о производной обратнойфункции: если y=f(x)и x=g(y)- две взаимно обратные возрастающие (или убывающие) функции, заданные на нек-рых интервалах, и существует конечная производная Односторонние производные. Если в точке х 0 существует предел
то он наз. правой производной функции y=f(x)' в точке х 0 (в этом случае нет необходимости требовать, чтобы функция была- определена всюду в нек-рой окрестности точки х 0;достаточно потребовать этого лишь для
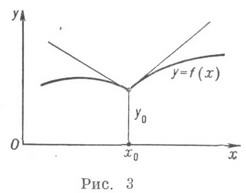
Функция f(x)имеет производную в точке х 0 в том и только в том случае, если в этой точке существуют равные между собой правая и левая производные. Для непрерывной функции существование в точке правой (соответственно левой) производной равносильно существованию в соответствующей точке ее графика правой (соответственно левой) односторонней полукасательной с угловым коэффициентом, равным значению этой односторонней производной. Точки, в к-рых полукасательные не образуют одну прямую, называются угловыми точками (см. рис. 3).
Производные высших порядков. Пусть функция y = f(x)имеет конечную производную y'=f' (х)в каждой точке нек-рого интервала; эта производная наз. также первой производной, или производной первого порядка, к-рая, будучи функцией от х, может, в свою очередь, иметь производную y"=f",(x), называемую второй производной, или производной второго порядка, функции f(x), и т. д. Вообще п-я производная, или производная порядка га, определяется по индукции равенством y{п)=(y(n-1))', в предположении, что y(n-1) определена на нек-ром интервале. При этом, наряду с y(n), используются также обозначения f(n) (х), Дифференциал. Пусть функция y - f(x)определена в нек-рой окрестности точки хи существует такое число А, что приращение Dy может быть представлено в виде Dy=ADx+w, где Функция y=f(x)имеет в точке хдифференциал в том и только в том случае, если она имеет в этой точке конечную производную Функция, для к-рой существует дифференциал, наз. дифференцируемой в рассматриваемой точке. Таким образом, дифференцируем ость функции означает одновременно и существование дифференциала, и существование конечной производной. При этом dy = df(x)=f'(x)Ax. Для независимого переменного хполагают dx= Ax и поэтому можно писать dy = f(x)dx, т. е. производная равна отношению дифференциалов:
См. также Дифференциал. Формулы и правила вычисления для производных приводят к соответствующим формулам и правилам вычисления для дифференциалов. В частности, справедлива теорема о дифференциале сложной функции: если функция y=f(u)дифференцируема в точке и 0, а функция j(х)дифференцируема в точке х 0, причем u0=ф(x0), то сложная функция у=f(j(x))дифференцируема в точке х 0 и dy=f(u0)du, где du=j'(x0)dx. Дифференциал сложной функции имеет точно такой же вид, как если бы переменное ибыло независимым. Это свойство наз. инвариантностью формы дифференциала. Однако, если и - независимое переменное, du=Аи есть произвольное приращение, а если и- функция, то du есть дифференциал этой функции, вообще говоря, не совпадающий с ее приращением. Дифференциалы высших порядков. Дифференциал dy наз. также первым дифференциалом, или дифференциалом первого порядка. Пусть y=f(x)- имеет дифференциал dy=f'(x)dx в каждой точке нек-рого интервала. Здесь dx= Ах- некоторое число, не зависящее от х, и поэтому можно считать dx=const. При этом dy оказывается функцией только от x и, в свою очередь, может иметь дифференциал, к-рый наз. вторым дифференциалом, или дифференциалом второго порядка функции f(x), и т. д. Вообще, п-й дифференциал, или дифференциал п-т о порядка, определяется по индукции равенством dny=d(dn-1y )в предположении, что дифференциал dn-1y определен в нек-ром интервале и что значение dx одно и то же на всех шагах. Свойство инвариантности для d2y, d3y,. . ., вообще говоря, не имеет места (исключение составляет y=j(u), где и- линейная функция). Повторный дифференциал от dy имеет вид продолжение Дифференциальное исчесление... Основные теоремы и приложения Д. и. К основным теоремам Д. и. для функций одного переменного обычно относят Ролля теорему, Лагранжа теорему (о конечном приращении), Коши теорему и Тейлора формулу. Эти теоремы лежат в основе наиболее важных приложений Д. и. к исследованию свойств функций - таких, как возрастание и убывание функции, выпуклость и вогнутость графика, к отысканию экстремумов, перегиба точек, асимптот графика. Д. и. позволяет вычислять пределы функций во многих случаях, когда простейшие теоремы о пределах не позволяют сделать этого (см. Неопределенностей раскрытие). Д. и. находит широкие приложения во мно- . гих разделах математики, в частности в геометрии. Д. и. функций многих переменных. Для простоты рассматривается случай функций двух переменных (за нек-рым исключением), хотя все понятия легко распространяются на случай трех и большего числа переменных. Пусть функция z=f(x, у )задана в нек-рой окрестности точки ( х 0, у 0 )и пусть зафиксировано значение y=y0. Тогда f(x, y0 )есть функция только от х. Если она имеет в х 0 производную по х, то эта производная наз. частной производной функции f( х, у) по х в точке ( х 0, у 0 )и обозначается f'x( х 0, у 0)>
где Dxz=f(x0+Dx, y0)-f(x0, y0) - частное приращение функции по х(dz/dx в общем случае нельзя рассматривать как дробь; д/дх есть символ операции). Аналогично определяется частная производная по у:
где DyZ - частное приращение функции по у.. Другие обозначения: Частными дифференциалами функции z - f(x, у )в точке ( х 0, у 0) ваз. (соответственно) выражения
(где, как и в случае одного переменного, dx=Dx, dy=Dyозначают приращения независимых переменных). Первые частные производные
Вместо d2z/dx2 употребляют также обозначения
вместо д 2z/дхду- обозначения
и т. д. Подобным образом вводятся частные производные третьего порядка и выше, и соответствующая символика: dnz/dxn- функция z дифференцируется праз по х; dnz/dxpdyq, где n=p+q,- функция z дифференцируется рраз по хи qраз по у. Частные производные второго и высших порядков, являющиеся результатом дифференцирования по разным переменным, наз. смешанными частными производными. Каждой частной производной отвечает нек-рый частный дифференциал, получаемый умножением ее на дифференциалы независимых переменных, взятые в степенях, равных числу дифференцирований по соответствующему переменному. Так получаются п-е частные дифференциалы, или частные дифференциалы n-го порядка:
Справедлива следующая важная теорема о смешанных производных: если в нек-рой окрестности точки ( х 0, у 0 )функция z=f(x, у )имеет смешанные частные производные f"xy(x, у )и f"yx(x, у )и эти производные непрерывны в точке ( х 0, у 0), то f"xy ( х 0, у 0) = f"yx( х 0, у 0). Функция z=f(x, у )наз. дифференцируемой в точке ( х 0, у 0 )по совокупности переменных х и у, если она определена в нек-рой окрестности этой точки и ее полное приращение
может быть представлено в виде
где Аи В- некоторые числа, w/r->0 при r=
наз. полным дифференциалом (первого порядка) функции f(x, у )в точке ( х 0, у 0);это есть главная линейная часть приращения. Функция, дифференцируемая в точке, непрерывна в этой точке (обратное не всегда верно!). Более того, дифференцируемость влечет существование конечных частных производных
Таким образом, для функции, дифференцируемой ( х 0, у 0).
или
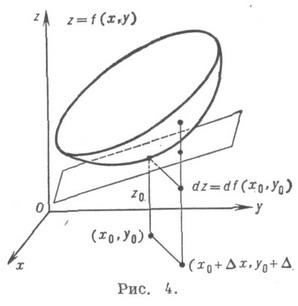
если, подобно случаю одного переменного, положим для независимых переменных dx=Dx, dy=Dy. Существование конечных частных производных общем случае не влечет ее дифференцируемоcти (здесь нарушается аналогия с функциями одного переменного). Достаточный признак дифференцируемости функции двух переменных: если в нек-рой окрестности точки ( х 0, у 0 )функция f(x, у )имеет конечные частные производные fx(x, у )и f'y(x, y), непрерывные в точке ( х 0, у 0), то f дифференцируема в этой точке. Геометрически полный дифференциал df(x0, y0 )есть приращение аппликаты касательной плоскости к поверхности z=f(x,y )в точке (х 0, у 0, z0), где z0=f( х 0, у 0 )(см. рис. 4). Полные дифференциалы высших порядков, подобно случаю функций одного переменного, вводятся по индукции равенством
в предположении, что дифференциал dn-1z определе в нек-рой окрестности рассматриваемой точки и что приращения аргументов dx, dy берутся одни и те же на всех шагах. Аналогично определяются и повторные дифференциалы.
Производные и дифференциалы сложных функций: Пусть w=f(u1, . . ., и т) - функция тпеременных, дифференцируемая в каждой точке открытой области Dm-мерного евклидова пространства Rm, и пусть тфункций u1=j1(x1, ..., х п) ..., um=jm(x1, ... , xn)- от n переменных заданых открытой области Gn-мерного евклидова пространства Rn. Пусть, наконец, точка (u1, . .., и т), соответствующая точке Тогда справедливы следующие теоремы: 1) Если функции j1, . . ., jm имеют конечные частные производные по х 1,..., х п, то сложная функция w=f(u1, ..., и т )от х 1, ..., х п также имеет конечные частные производные по x1 , ..., х п и
2) Если функции j1, ...,jm дифференцируемы по совокупности переменных x1, ..., х п в точке
где du1,-, dum -дифференциалы функций u1,... и т. Таким образом, свойство инвариантности первого дифференциала имеет место и для функций нескольких переменных. Для дифференциалов второго и высших порядков это свойство, вообще говоря, нарушается. Д. и. применяется к изучению свойств функций многих переменных: к отысканию экстремумов, к исследованию функций, задаваемых одним или несколькими неявными уравнениями, к теории поверхностей и т. д. Одним из главных инструментов при этом является Тейлора формула. Понятия производной и дифференциала и их простейшие свойства, связанные с арифметич. действиями над функциями и суперпозицией функций, включая свойство инвариантности первого дифференциала, почти без изменений распространяются на комплексные функции одного или нескольких действительных переменных, на действительные и комплексные вектор-функции одного или нескольких действительных переменных, на комплексные функции и вектор-функции одного или нескольких комплексных переменных. В функциональном анализе понятия производной и дифференциала распространяются на функции точки абстрактного пространства. Лит.:История дифференциального и интегрального исчисления - [1] История математики с древнейших времен до начала XIX столетия, т. 1-3, М., 1970 - 72; [2] Рыбников К. А., История математики, т. 1-2,М., 1960-63; [3] Вилейтнер Г., История математики от Декарта до середины XIX столетия, пер. с нем., 2 изд., М., 1966; [4] Стройк Д. Я., Краткий курс истории математики, пер. с нем., 2 изд., М., 1969; [5] Бурбаки Н., Очерки по истории математики, пер. с франц., М., 1963; [6] Сantоr М., Vorlesungen tiber Geschichte der Mathematik, 2 Aufl., Bd 1-4, Lpz., 1000-08. Работы основоположников и классиков дифференциального и интегрального исчисления - [7] Ньютон И., Математические работы, пер. с латин., М.- Л., 1937; [8] Лейбниц Г., Избранные отрывки из математических сочинений, пер. с латин., "Успехи матем. наук", 1948, т. 3, в. 1; [9] Л'Опиталь Г. Ф. де, Анализ бесконечно малых, пер. с франц., М.- Л., 1935; [10] Эйлер Л., Введение в анализ бесконечных, пер. с латин., 2 изд., т. 1, М., 1961; [11] его же, Дифференциальное исчисление, пер. с латин., М.-Л., 1949; [12] Коши О. Л., Краткое изложение уроков о дифференциальном и интегральном исчислении, пер. с франц., СПБ, 1831; [13] его же, Алгебраический анализ, пер. с франц., Лейпциг. 1864. Учебники и учебные пособия по дифференциальному и интегральному исчислению - [14] Гурса Э., Курс математического анализа, пер. с франц., 3 изд., т. 1, М.-Л., 1936; [15] Ла Валле Пуссен Ш. Ж. де, Курс анализа бесконечно малых, пер. с франц., т. 1, Л.-М., 1933; [16] Курант Р., Курс дифференциального и интегрального исчисления, пер. с нем. и англ., 4 изд., т. 1, М., 1967; [17] Рудин Р., Основы математического анализа, пер. с англ., М., 1966; [18] Ильин В. А., Позняк Э. Г., Основы математического анализа, т. 1, 3 изд., М., 1971; т. 2, 1973; [19] Кудрявцев Л. Д., Математический анализ, 2 изд., М., 1973; [20] Никольский С. М., Курс математического анализа, 2 изд., М., 1975; [21] Толстов Г. П., Элементы математического анализа, т. 1-2,2изд.,М., 1974; [22] Смирнов В. И., Курс высшей математики, 22 изд., т. 1, М., 1967; [23] Фихтеягольц Г. М., Курс дифференциального и интегрального исчисления, 7 изд., М., 1969; [24] Хинчин А. Я., Восемь лекций по математическому анализу, 3 изд., М.- Л., 1948. Г. П. Толстое. |
|
|
|

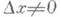 есть приращение аргумента, Dy=f(x0+Dx)-f(x0).- соответствующее приращение функции. Если существует (конечный или бесконечный) предел
есть приращение аргумента, Dy=f(x0+Dx)-f(x0).- соответствующее приращение функции. Если существует (конечный или бесконечный) предел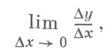
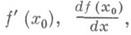 у', у' х,
у', у' х, 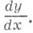 Итак, по определению,
Итак, по определению,
 произвольным образом стремится к точке М). Если упомянутая касательная существует, то она - единственна. Если положить х=х 0+D х, Ay=f(x0+Dx)- f(x0), то для угла b между МР и положительным направлением оси Ох будет иметь место равенство
произвольным образом стремится к точке М). Если упомянутая касательная существует, то она - единственна. Если положить х=х 0+D х, Ay=f(x0+Dx)- f(x0), то для угла b между МР и положительным направлением оси Ох будет иметь место равенство  (см. рис. 1). Кривая Симеет в точке Мкасательную в том и только в том случае, если существует
(см. рис. 1). Кривая Симеет в точке Мкасательную в том и только в том случае, если существует  т. е, существует f'( х 0). При этом для угла a. между касательной и положительным направлением оси Ох справедливо равенство tga=f'(x0). В случае конечной производной f'(х 0) касательная образует с Ох острый угол, т. е.
т. е, существует f'( х 0). При этом для угла a. между касательной и положительным направлением оси Ох справедливо равенство tga=f'(x0). В случае конечной производной f'(х 0) касательная образует с Ох острый угол, т. е.
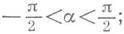 в случае
в случае 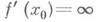 касательная образует с Ох прямой угол (см. рис. 2). Таким образом, производная непрерывной функции f(x)в точке х 0 совпадает с угловым коэффициентом tga касательной к кривой, заданной уравнением у=f(x), в ее точке с абсциссой х 0.
касательная образует с Ох прямой угол (см. рис. 2). Таким образом, производная непрерывной функции f(x)в точке х 0 совпадает с угловым коэффициентом tga касательной к кривой, заданной уравнением у=f(x), в ее точке с абсциссой х 0. т. е. u=f'(t). (в предположении, что эта производная существует).
т. е. u=f'(t). (в предположении, что эта производная существует).

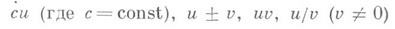
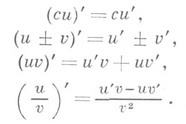
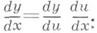
 то в точке y0=f(z0 )существует конечная производная
то в точке y0=f(z0 )существует конечная производная 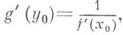 или, в другой записи,
или, в другой записи, 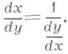 Эта теорема допускает обобщение: если, при выполнении прочих условий, f' (x0) =0(f' ( х о)=
Эта теорема допускает обобщение: если, при выполнении прочих условий, f' (x0) =0(f' ( х о)= ), то g'( у о)=
), то g'( у о)=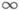 (соответственно g'( у 0)=0).
(соответственно g'( у 0)=0).
 ). Аналогично определяется левая производная - как предел
). Аналогично определяется левая производная - как предел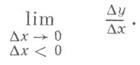
 , а для n=2, 3 еще у", f" (х), у'", f'"(х). Вторая производная имеет механич. истолкование: это есть ускорение
, а для n=2, 3 еще у", f" (х), у'", f'"(х). Вторая производная имеет механич. истолкование: это есть ускорение  в момент tточки, движущейся прямолинейно по закону s=f(t).
в момент tточки, движущейся прямолинейно по закону s=f(t). при
при  Член А Ах в этой сумме обычно обозначается символом dy, или df(x), и наз. дифференциалом функции f(x)(по переменному х)в точке х. Дифференциал есть главная линейная часть приращения функции (геометрически изображается отрезком LT на рис. 1, где МТ- касательная к кривой y=f(x)в рассматриваемой точке ( х 0, у 0)).
Член А Ах в этой сумме обычно обозначается символом dy, или df(x), и наз. дифференциалом функции f(x)(по переменному х)в точке х. Дифференциал есть главная линейная часть приращения функции (геометрически изображается отрезком LT на рис. 1, где МТ- касательная к кривой y=f(x)в рассматриваемой точке ( х 0, у 0)).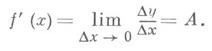

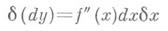 и вторым дифференциалом является значение d (dy )при dx=dx.
и вторым дифференциалом является значение d (dy )при dx=dx.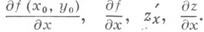 Итак, по определению,
Итак, по определению,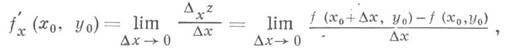

 Частные производные вычисляются по правилам дифференцирования функций одного переменного (при вычислении z'x нужно считать у=const, а при вычислении z'y- считать х=const).
Частные производные вычисляются по правилам дифференцирования функций одного переменного (при вычислении z'x нужно считать у=const, а при вычислении z'y- считать х=const).
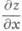 =f'x( х, у) и
=f'x( х, у) и 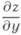 =f'y(x, у), или частные производные первого порядка, являясь функциями от x и у, могут в свою очередь иметь частные производные по хи у, к-рые называются, по отношению к функции z=f(x, у), частными производными второго порядка, или вторыми частными производными. При этом полагают
=f'y(x, у), или частные производные первого порядка, являясь функциями от x и у, могут в свою очередь иметь частные производные по хи у, к-рые называются, по отношению к функции z=f(x, у), частными производными второго порядка, или вторыми частными производными. При этом полагают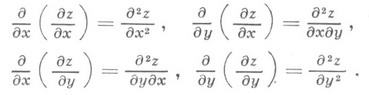
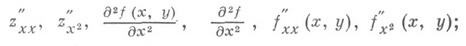
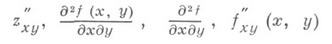
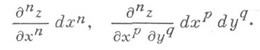
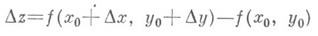
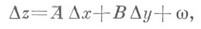
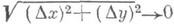 (при условии, что точка (x0+ D х, у 0+Dу)принадлежит упомянутой окрестности). При этом выражение
(при условии, что точка (x0+ D х, у 0+Dу)принадлежит упомянутой окрестности). При этом выражение
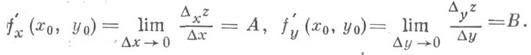
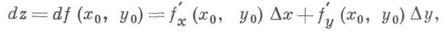
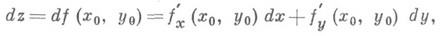
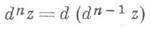
 не выходит из области D
не выходит из области D
 то и сложная функция w=f(u1, ... , и т) дифференцируема в этой точке и
то и сложная функция w=f(u1, ... , и т) дифференцируема в этой точке и