|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ДИФФЕРЕНЦИАЛЬНО-ГЕОМЕТРИЧЕСКАЯ СТРУКТУРАЗначение ДИФФЕРЕНЦИАЛЬНО-ГЕОМЕТРИЧЕСКАЯ СТРУКТУРА в математической энциклопедии: - одно из основных понятий современной дифференииальной геометрии, включающее конкретные изучаемые в ней структуры. Д.-г. с. определяется для данного дифференцируемого многообразия М п как дифференцируемое сечение в расслоенном пространстве( Х F, pF, М n )с базой М п, ассоциированном с нек-рым главным расслоением (X, р, М п), или, в другой терминологии, как дифференцируемое поле нек-рого геометрич. объема на М n. Здесь Fявляется нек-рым дифференцируемым Если (X, р, М n).- главное расслоение реперов в касательных к М п пространствах, G- нек-рая замкнутая подгруппа в Важными частными случаями Д.-г. с. являются связности. Напр., связность в главном расслоении получается, если в роли М n выступает пространство нек-рого главного расслоения ( Р, р, В), а G-структуро на Рявляется такое распределение m-мерных, m=dim P-dimB, подпространств, дополнительных к касательным пространствам слоев, к-рое инвариантно относительно действия в Рструктурной группы расслоения. Связности на многообразии М п являются частными случаями Д.-г. с. на М п, но более общими, чем G-cтpyктуры на М п. Напр., аффинная связность на М п, к-рую можно определить полем объекта связности
здесь
- координаты элемента группы Лит.:[1] Вагнер В. <В., [Дополнение], в кн.: Веблен О. Уайтхед Дж., Основания дифференциальной геометрии, пер с англ., М., 1949, с. 135-223; [2] Лаптев Г. Ф., "Тр. Моск матем. об-ва", 1953, т. 2, с. 275-382; [3]Хьюзмоллер Д. Расслоенные пространства, пер. с англ., М., 1970; [4] Стерн берг С, Лекции по дифференциальной геометрии, пер. англ., М., 1970. Ю. Г. <Лумисте |
|
|
|
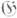-пространством, где (V - структурная группа Ли главного расслоения (X, р, М п), или, в другой терминологии, пространством представления группы Ли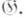 
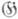=GL(n, R), a F- однородное пространство 
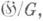то соответствующая Д.-г. с. на М п наз. G-c труктурой, или инфинитезимальной структурой 1-го порядка. Напр., если Gсостоит из всех таких линейных преобразований (элементов из GL(n,R).), к-рые оставляют инвариантным m-мерное пространство в Rn, то соответствующая G-структура определяет на М п распределение m-мерных подпространств. Если Gявляется ортогональной группой 
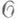(и, R) - подгруппой элементов из GL(n,R), сохраняющих скалярное произведение в Rn, то G- структура есть риманова метрика на М п, т. е. поле положительно определенного симметр:;ч. тензора gij. Аналогично, частными случаями G-структуры на М п являются почти комплексная и комплексная структуры. Обобщением G-структуры является инфинитезимальная структура r-го порядка r>1 (или G-структура высшего порядка); здесь (X, р) М n )является главным расслоением реперов r-порядка на М п,a G - замкнутой подгруппой eго структурной группы Dnr.
получается как Д.-г. с. на М п, при к-рой (X, р, М n )является главным расслоением реперов 2-го порядка,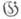 
- его структурной группой D2n а пространство Fпредставления группы Dn- пространством R3n с координатами 
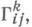где представление определяется формулами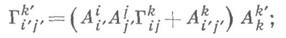
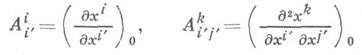
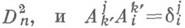В случае проективной связности на Mn имеют дело с нек-рым представлением группы Dв пространстве R3(n+1), а в случае связностей высшего порядка - с представлениями группы 
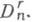При таком подходе теория Д.-г. с. имеет самый тесный контакт с геометрических объектов теорией.