|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
АЛГОРИТМОВ ТЕОРИЯЗначение АЛГОРИТМОВ ТЕОРИЯ в математической энциклопедии: раздел математики, изучающий общие свойства алгоритмов. Содержательные явления, приведшие к образованию понятия "алгоритм", прослеживаются в математике в течение всего времени ее существования. Однако само это понятие сформировалось лишь в 20 в. и стало предметом самостоятельного изучения (по-видимому, впервые, хотя еще в расплывчатом виде) в 20-х гг. 20 в. в трудах представителей интушионизма Л. Э. Я. Брауэра (L. Е. J. Brouwer) и Г. Вейля (Н. Weyl, см. [1]). Началом сиотематич. разработки А. т. можно считать 1936, когда А. Чёрч (A. Church, [2]) опубликовал первое уточнение понятия вычислимой функции (предложив отождествлять понятие всюду определенной вычислимой функции, имеющей натуральные аргументы и значения, с понятием общерекурсивной функции) и привел первый пример функции, не являющейся вычислимой, а А. М. Тьюринг (А. М. Turing, [3], [4]) и Э. Л. Пост (Е. L. Post, [5]) дали первые уточнения понятия алгоритма (в терминах идеализированных вычислительных машин, см. Тьюринга машина). В дальнейшем А. т. получила развитие в трудах С. К. Клини (S. С. Kleene), Э. <Л. Поста (см. [6] - [8]), А. А. Маркова (см. [9] - [11]) п др. В частности, А. А. Марков предложил уточнять понятие алгоритма с помощью введенного им понятия нормального алгорифма (си. [10]). Наиболее общий подход к уточнению понятия алгоритма предложил А. Н. Колмогоров (см. [12], [13]). Поскольку алгоритмы могут иметь дело лишь с так наз. конструктивными объектами, то, чтобы перенести понятия и методы А. т. на случай неконструктивных объектов, надо эти последние объекты обозначить, или поименовать, конструктивными объектами. Изучение общих свойств таких поименований (прежде всего, когда в качестве обозначений, или имен, выступают натуральные числа) составляет предмет теории нумерации (см. [14]), образующей важный раздел А. т. Основные понятия теории алгоритмов. Областью применимости алгоритма наз. совокупность тех объектов, к к-рым он применим. Про алгоритм говорят, что он: 1) "вычисляет функцию f", коль скоро его область применимости совпадает с областью определения Детальный анализ понятия "алгоритм" обнаруживает, что: (I) область возможных исходных данных и область применимости любого алгоритма суть перечислимые множества. В свою очередь, (II) для любой пары вложенных одно в другое перечислимых множеств можно подобрать алгоритм, у к-рого большее множество служит областью возможных исходных данных, а меньшее- областью применимости. Имеют место следующие основные теоремы: (III) функция f вычислима тогда и только тогда, когда перечислим ее график, т. е. множество всех пар вида Алгоритмические проблемы. Проблема построения алгоритма, обладающего теми или иными свойствами, наз. алгоритмической проблемой (а. п.). Как правило, свойство искомого алгоритма формулируется в терминах свойств того соответствия, к-рое должно иметь место между исходными данными п результатами алгоритма. Важные примеры а. п.: проблема вычисления данной функции (требуется построить алгоритм, вычисляющий эту функцию); проблема разрешения данного множества (требуется построить алгоритм, разрешающий это множество относительно нек-poro другого множества); проблема перечисления данного множества (требуется построить алгоритм, перечисляющий данное множество). Все примеры а. п. из различных областей математики, названные ниже в разделе "Приложения", являются проблемами разрешения. Неразрешимость а. п. означает отсутствие соответствующего алгоритма; теоремы, устанавливающие неразрешимость таких проблем, относятся к числу наиболее важных теорем А. т. Так, для алгоритма с неразрешимой областью применимости неразрешима а. п. разрешения этой области относительно области возможных исходных данных. Посредством сведения к неразрешимости этой проблемы была установлена неразрешимость большинства других проблем разрешения (в частности, всех проблем, указанных ниже в разделе "Приложения"). Вопрос о том, для любой ли неразрешимой проблемы разрешения ее неразрешимость может быть установлена таким способом, составляет так наз. проблему алгоритмической сводимости. Метрическая теория алгоритмов. А. т. можно разделить на дескриптивную (качественную) и метрическую (количественную). Первая - исследует алгоритмы с точки зрения устанавливаемого ими соответствия между исходными данными и результатами; к ней относятся, в частности, те алгоритмич. проблемы, о к-рых говорилось в предыдущем разделе. Вторая - исследует алгоритмы с точки зрения сложности как самих алгоритмов (см. Алгоритма сложность), так и задаваемых ими "вычислений", то есть процессов последовательного преобразования конструктивных объектов. Важно подчеркнуть, что как сложность алгоритмов, так и сложность вычислений могут определяться различными способами, причем может оказаться, что при одном способе Абудет сложнее В, а при другом способе - наоборот. Чтобы говорить о сложности алгоритмов, надо сначала описать к.-л. точный язык для записи алгоритмов и затем под сложностью алгоритма понимать сложность его записи; сложность же записи можно определять различными способами (напр., как число символов данного типа, участвующих в записи, или как набор таких чисел, вычисленных для разных типов символов). Чтобы говорить о сложности вычисления, надо уточнить, как именно вычисление представляется в виде цепочки сменяющих друг друга конструктивных объектов и что считается сложностью такой цепочки (только ли число членов в ней - "число шагов" вычисления, или еще учитывается "размер" этих членов и т. п.); в любом случае сложность вычисления зависит от исходного данного, с к-рого начинается вычисление, поэтому сложность вычисления есть функция, сопоставляющая с каждым объектом пз области применимости алгоритма сложность соответствующей цепочки. Разработка методов оценки сложности алгоритмов и вычислений имеет важное теоретич. ы практпч. значение, однако в отличие от дескриптивной А. т., оформившейся в целостную математич. дисциплину (см. [11], [15], [16]), метрич. А. т. находится в процессе становления (см. [17] - [20]). Приложения теории алгоритмов имеются во всех областях математики, в к-рых встречаются алгоритмпч. проблемы. Такие проблемы возникают в математической логике и моделей теории;для каждой теории формулируется проблема разрешения множества всех истинных или доказуемых предложений этой теории относительно множества всех ее предложений (теории подразделяются на разрешимые и неразрешимые - в зависимости от разрешимости или неразрешимости указанной проблемы); в 1936 А. Чёрч (см. [21] , [22]) установил неразрешимость проблемы разрешения -для множества всех истинных предложений логики предикатов, дальнейшие важные результаты в этом направлении принадлежат А. Тарскому (A. Tarski), А. И. Мальцеву и др. (см. [23]). Неразрешимые алгоритмич. проблемы встречаются в алгебре (проблема тождества для полугрупп и, в частности, для групп); первые примеры полугрупп с неразрешимой проблемой тождества были найдены в 1947 независимо А. А. Марковым (см. [9]) и Э. Л. Постом (см. [8]), а пример группы с неразрешимой проблемой тождества - в 1952 П. С. Новиковым (см. [24], [25]); в топологии (проблема гомеоморфии, неразрешимость к-рой для важного класса случаев была доказана в 1958 А. А. Марковым, (см. [26]); в теории чисел (проблема разрешимости диофантовых уравнений, неразрешимость к-рой была установлена в 1970 Ю. В. Матия-севичем, (см. [27], [28]) и др. разделах математики. А. т. тесно связана с математич. логикой, поскольку на понятие алгоритма опирается одно из центральных понятии математич. логики - понятие исчисления, и потому, напр., Гёделя теорема о неполноте формальных систем может быть получена как следствие теорем А. т. (см. [29]). Наконец, А. т. тесно связана с основаниями математики, в к-рых одно из центральных мест занимает проблема соотношения конструктивного и неконструктивного; в частности, А. т. дает аппарат, необходимый для разработки конструктивного направления в математике; в 1965 А. Н. Колмогоров предложил использовать А. т. для обоснования теории информации (см. [30], Алгоритмическая теория информации). А. т. образует теоретич. фундамент для ряда вопросов вычислительной математики и тесно связана с кибернетикой, в которой важное место занимает изучение алгоритмов управления. Лит.:[1] Вейль Г., О философии математики, пер. с нем., М.- Л., 1934; [2] Church A., "Amer. J. Math.", 1936, v. 58, № 2, p. 345-63; [3] Turing A. M., "Proc. London Math. Soc.", ser. 2, 1936, v. 42, №№ 3-4, p. 230-65; [4] его же, там же, 1937, v. 43, № 7, p. 544-46; [5] Pоst E. L., "J. Symbol. Log.", 1936, v. 1, № 3, p. 103-05; [6] его же, "Amer. J. Math.", 1943, v. 65, № 2, p. 197-215; [7] его же, "Bull. Amer. Math. Soc.", 1944, v. 50, № 5, p. 284-316; [8] его же, "J. Symbol. Log.", 1947, v. 12, № 1, p. 1-11; [9]Mapков А. А., "Докл. АН СССР", 1947, т. 55, № 7, с. 587-90; [10] его же, "Тр. Матем. ин-та АН СССР", 1951, т. 38, с. 176-89; [11] его же, Теория алгорифмов, М.- Л., 1954; [12] Колмогорова. Н., "Успехи матем. наук", 1953, т. 8, № 4, с. 175-76; [13] Колмогоров А. Н., Успенский В. А., там же, 1958, т. 13, К" 4, с. 3-28; [14] Ершов Ю. Л., Теория нумераций, ч. 1-2, Новосибирск, 1969-73; [15] Мальцев А. И., Алгоритмы и рекурсивные функции, М., 1965; [16] Роджерс X., Теория рекурсивных функций и эффективная вычислимость, пер. с англ., М., 1972; [17] Марков А. А., "Изв. АН СССР. Сер. матем.", 1967, т. 31, № 1, с. 161-208; [18] Трахтенброт Б. А., Сложность алгоритмов и вычислений, Новосибирск, 1967; [19] Проблемы математической логики. Сложность алгоритмов и классы вычислимых функций, сб. переводов, М., 1970; [20] Сложность вычислений и алгоритмов, сб. переводов, М., 1974; [21] Church A., "J. Symbol. Log.", 1936, v. 1, Т 1, p. 40-41; [22] его же, там же, № 3, р. 101-02; [23] Ершов Ю. Л., Лавров И. А., Тайманов А. Д., Тайцлин М. А., "Успехи матем. наук", 1965, т. 20, № 4, с. 37-108; [24] Новиков П. С., "Докл. АН СССР", 1952, т. 85, с. 709-12; [25] его ж е, Об алгоритмической неразрешимости проблемы тождества слов в теории групп, М., 1955; [26] Марков А. А., "Докл. АН СССР", 1958, т. 121, № 2, с. 218-20; [27] Матиясевич Ю. В., там же, 1970, т. 191, №2, с. 279-82; [28] его же, "Успехи матем. наук", 1972, т. 27, №5, с. 185-222; [29] Успенский В. А., там же, 1974, т. 29, № 1, с. 3-47; [30] Колмогоров А. Н., "Проблемы передачи информации", 1965, т. 1, № 1, с. 3 -Н. В. <А. <Успенский. |
|
|
|

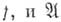 перерабатывает всякий хиз своей области применимости в
перерабатывает всякий хиз своей области применимости в  ; 2) "разрешает множество Аотносительно множества X", коль скоро он применим ко всякому
; 2) "разрешает множество Аотносительно множества X", коль скоро он применим ко всякому  из
из  и перерабатывает всякий
и перерабатывает всякий  из
из  в слово "да", а всякий х из
в слово "да", а всякий х из . в слово "нет"; 3) "перечисляет множество В", коль скоро его область применимости есть натуральный ряд, а совокупность результатов есть В. Функция наз. вычислимой, если существует вычисляющий ее алгоритм. Множество наз. разрешимым относительно X, если существует разрешающий его относительно Xалгоритм. Множество наз. перечислимым, если либо оно пусто, либо существует перечисляющий его алгоритм.
. в слово "нет"; 3) "перечисляет множество В", коль скоро его область применимости есть натуральный ряд, а совокупность результатов есть В. Функция наз. вычислимой, если существует вычисляющий ее алгоритм. Множество наз. разрешимым относительно X, если существует разрешающий его относительно Xалгоритм. Множество наз. перечислимым, если либо оно пусто, либо существует перечисляющий его алгоритм. . (IV) Подмножество Аперечислимого множества Xтогда и только тогда разрешимо относительно X, когда Аи
. (IV) Подмножество Аперечислимого множества Xтогда и только тогда разрешимо относительно X, когда Аи  перечислимы. (V) Если Аи В перечислимы, то
перечислимы. (V) Если Аи В перечислимы, то  и
и  также перечислпмы. (VI) В каждом бесконечном перечислимом множестве Xсуществует перечислимое подмножество с неперечислимым дополнением [в силу (IV) это перечислимое подмножество будет неразрешимым относительно Х].(VII) Для каждого бесконечного перечислимого множества Xсуществует вычислимая функция, определенная на подмножестве этого множества и не продолжаемая до вычислимой функции, определенной на всем X. Утверждения (VI) и (II) в совокупности дают упоминаемый в статье Алгоритм пример алгоритма с неразрешимой областью применимости. Разрешимые и перечислимые множества составляют простейшие (и наиболее важные) примеры множеств, строение к-рых задается с помощью тех или иных алгоритмич. процедур. Систематич. изучение множеств конструктивных объектов с точки зрения таких свойств этих множеств, к-рые связаны с наличием тех или иных алгоритмов, образует так наз. алгоритмическую теорию множеств; нек-рые понятия, методы и результаты этой теории находят глубокие аналогии в дескриптивной теории множеств.
также перечислпмы. (VI) В каждом бесконечном перечислимом множестве Xсуществует перечислимое подмножество с неперечислимым дополнением [в силу (IV) это перечислимое подмножество будет неразрешимым относительно Х].(VII) Для каждого бесконечного перечислимого множества Xсуществует вычислимая функция, определенная на подмножестве этого множества и не продолжаемая до вычислимой функции, определенной на всем X. Утверждения (VI) и (II) в совокупности дают упоминаемый в статье Алгоритм пример алгоритма с неразрешимой областью применимости. Разрешимые и перечислимые множества составляют простейшие (и наиболее важные) примеры множеств, строение к-рых задается с помощью тех или иных алгоритмич. процедур. Систематич. изучение множеств конструктивных объектов с точки зрения таких свойств этих множеств, к-рые связаны с наличием тех или иных алгоритмов, образует так наз. алгоритмическую теорию множеств; нек-рые понятия, методы и результаты этой теории находят глубокие аналогии в дескриптивной теории множеств.