|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ДИСПЕРСИОННЫЙ МЕТОДЗначение ДИСПЕРСИОННЫЙ МЕТОД в математической энциклопедии: в теории чисел- метод для решения нек-рых бинарных уравнений (бинарных аддитивных проблем )вида
где a и b принадлежат к достаточно густым и хорошо распределенным в арифметич. прогрессиях последовательностям натуральных чисел. Д. м., разработанный Ю. В. Линником в 1958-61 и поэтому называемый также дисперсионным методом Линника, соединяет в себе элементарные теоретико-вероятностные понятия (в частности, понятие дисперсии и неравенства типа Чебышева) с аналитич. и алгебраич. идеями И. М. Виноградова иА. Вейля (A. Weil). Сущность Д. м. состоит в следую щем (см. также Аддитивная теория чисел). Уравнение (1) сводится к уравнениям вида
здесь v, D' независимо пробегают нек-рые значения из прямоугольной области Пусть теперь имеется уравнение
Оценкаразности F-S= V имеет вид
Применение неравенства Коши приводит к неравенству
где D0- длина интервала (D), а
есть дисперсия числа решений уравнения (2). Если распространить суммирование в (5) на все D
Суммы е 1, е 2 и е 3 в нек-рых случаях удается вычислить асимптотически. Главную трудность представляет вычисление е 1 - основной суммы Д. м. Асимптотич. расчет суммы е 1 осуществляется при помощи Виноградова метода по подсчету для нек-рых функций количества их дробных частей, попадающих в заданный сегмент, а также с использованием новейших оценок тригонометрич. сумм, полученных средствами алгебраич. геометрии. Асимптотика для сумм е 2 и е 3 находится путем элементарного суммирования. Если, в результате, дисперсия оказывается не слишком большой, то из (3) и (4) получается асимптотика для числа решений уравнения (2). Объединение числа решений всех уравнений вида (2) приводит к асимптотич. формуле для числа решений уравнения (1). Рассмотренная схема Д. м. применима и для решения уравнений вида
где l- заданное целое число, отличное от нуля. При помощи этого метода Ю. В. Линником и др. (см. [3]) был решен ряд классических бинарных аддитивных проблем, к-рые до создания Д. м. могли быть решены только на основе эвристических или гипотетических соображений. К числу таких проблем относятся: аддитивная проблема делителей(a=х 1, х 2 . . . xk, k = const, b=xy); Титчмарша проблема делителей (a=р - простое, b=xy); Харди- Литлвуда проблема(a=р- простое, b=x2+y2). При помощи Д. м. решены также нек-рые аналоги и обобщения этих проблем, в частности найдена асимптотика для числа решений общего уравнения Харди - Литлвуда: р+j(x, h))=n, где р- простое, а j(x, h) - заданная примитивная положительно определенная квадратичная форма. Доказано существование бесконечного множества простых чисел вида p=j(x, h)+l, где Область применения Д. м. пересекается с областью применения метода большого решета Ю. В. Линника. Лит.:[1] Линник Ю. В., Дисперсионный метод в бинарных аддитивных задачах, Л., 1961; [2] Приложение 1 в кн.: Прахар К., Распределение простых чисел, пер. с нем., М., 1967; [3] Бредихин Б. М., "Успехи матем. наук", 1965, т. 20, в. 2, с. 89-130; [4] Бредихин Б. М., Линник Ю. В., в сб.: Актуальные проблемы аналитической теории чисел, Минск, 1974, с. 5-22. Б. М. Бредихин. |
|
|
|



 где (v) и (D)- некоторые интервалы; при этом числа v - простые, а на D' могут быть наложены различные дополнительные условия. Пусть через Fобозначено число решений этого уравнения.
где (v) и (D)- некоторые интервалы; при этом числа v - простые, а на D' могут быть наложены различные дополнительные условия. Пусть через Fобозначено число решений этого уравнения. при произвольном
при произвольном  и через ( п, D )обозначено число его решений, найденных из каких-либо эвристических соображений. Тогда (гипотетически) число ожидаемых решений уравнения (2) записывается в виде
и через ( п, D )обозначено число его решений, найденных из каких-либо эвристических соображений. Тогда (гипотетически) число ожидаемых решений уравнения (2) записывается в виде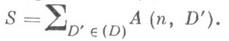
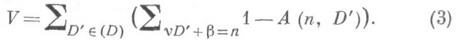


 (D), то будут сняты все дополнительные условия, наложенные на D' в (2). В то же время величина дисперсии может только возрасти. Поэтому
(D), то будут сняты все дополнительные условия, наложенные на D' в (2). В то же время величина дисперсии может только возрасти. Поэтому

 - любое фиксированное целое число.
- любое фиксированное целое число.