|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ДИРИХЛЕ Z-ФУНКЦИЯЗначение ДИРИХЛЕ Z-ФУНКЦИЯ в математической энциклопедии: Дирихле L-pяд, L-p яд, - функция комплексного переменного s=s+it, определяемая для всех Дирихле характеровc.mod d рядом
Д. L- ф .mod dкак функции действительного переменного s введены в 1837 П. Дирихле (P. Dirichlet, см. [1]) в связи с доказательством бесконечности простых чисел в арифметич. прогрессии dm+l, разность dи первый член lк-рой взаимно простые числа. Они представляют собой естественное обобщение - дзета-функции Римана z(s) на арифметич. прогрессии и служат мощным средством исследований в аналитич. теории чисел (см. [2] - [4]). Ряды (1), наз. Дирихле рядами, абсолютно и равномерно сходятся в любой конечной области комплексной s - плоскости, для к-рой
В силу ограниченности суммы под знаком интеграла эта формула осуществляет аналитическое продолжение L(s, x )как регулярной функции в полуплоскость s>0. Для любого c.mod dсправедливо представление L(s, x )в виде произведения Эйлера по простым числам р:
Отсюда, если c=c0- главный характер mod d, то при d=l L(s,c0) = z(s), а для d>l
Поэтому свойства L(s,c0). на всей комплексной плоскости в основном определяются свойствами z(s). В частности, функция L(s,c0) регулярна для всех s, кроме s=l, где она имеет простой полюс с вычетом d-1j(d), j - функция Эйлера. Если же
Тем самым в главном Д. L-ф. с характерами c неравно c0 сводятся к таковым для примитивных характеров. Это свойство Д. L =ф. играет существенную роль, так как многие результаты, касающиеся L(s,c), имеют простой вид лишь для примитивных характеров. В случае примитивного характера cmod dаналитич. продолжение на всю плоскость и функциональное уравнение функции L(s, x )получаются прямым обобщением метода Римана для z(s). Результат, если положить
имеет вид
где Г - гамма-функция, Распределение нетривиальных нулей, вообще значений L(s,X )в критич. полосе, является важнейшей проблемой теории Д. L-ф., имеющей фундаментальное значение для теории чисел. То, что каждая из функций L(s,c)имеет бесконечно много нетривиальных нулей и что законы распределения простых чисел в арифметич. прогрессиях находятся в прямой зависимости от расположения этих нулей, показывают соответствующие аналоги формул Римана. Именно, пусть N(T,c)- число нулей функции L(s,c)с примитивным c mod dв прямоугольнике 0<s<1 |t|<T,
Пусть
Тогда по свойству ортогональности характеров
где суммирование производится по всем характерам X mod d, и для c-примитивного характера c, a=1-d:
где r=b+ig пробегает нетривиальные нули L(s,c), V- производная Lпо s. Практически более полезны приближенные формулы для y(x; a): для произвольного
а для х=Хо
Последняя функция вносит в сумму (6) величину, представляющую главный член. Существует гипотеза, наз. расширенной гипотезой Римана, о том, что все нетривиальные нули Д. L-ф. лежат на прямой s=1/2. Если эта гипотеза справедлива, то для
и многие другие важные проблемы теории чисел получили бы свое окончательное решение. Однако вопросы, касающиеся расположения нетривиальных нулейД. L-ф. исключительно трудны и в настоящее время (1978) в этом отношении известно сравнительно немного, причем для комплексных характеров получены более сильные результаты,, чем для действительных. Обобщением метода, указанного в 1899 III. Ж. Балле Пуссеном для функции z(s), получена граница нетривиальных нулей L(s,c):. Для комплексного характера X mod dсуществует абсолютная постоянная Стакая, что L(s,c) не имеет нулей в области
Последняя известная граница для b указана в 1935К. Эйфелем (С. Siegel): при любом e>0 существует положительное число С(e) такое, что
Эта оценка имеет однако существенный недостаток, она является неэффективной в том смысле, что по заданному e нельзя оценить численное значение постоянной С(e). Таким же недостатком страдают и теоретико-числовые результаты, вывод к-рых опирается на оценку Зигеля. Вследствие указанных границ для нетривиальных нулей Д. L-ф. и формул (6) - (8) справедлив асимптотич. закон распределения простых чисел в виде:
Эти результаты являются лучшими в проблеме равномерного распределения простых чисел в арифметич. прогрессиях растущей разности d. Для фиксированных значений dизвестно несколько больше. В таком случае теория Д. L-ф. при
где С- положительная постоянная, зависящая от d. Этой границе нетривиальных нулей Д. L-ф. фиксированного mod d отвечает лучший (1977) остаточный член в асимптотич. формуле для y(x; d, l )в виде:
Все формулы относительно асимптотики функции y(x; d, l )имеют аналоги для функции p(х; d, l) - числа простых чисел К числу основных направлений исследований в современной теории Д. L-ф. относятся также исследования плотности распределения нетривиальных нулей Д. L-ф., содержание к-рых составляют оценки величин:
где N(s, T,c)обозначает число нулей L(s,c)в прямоугольнике Лит.:[1] Дирихле П. Г. Л., Лекции по теории чисел, пер. с нем., М.-Л., 1936; [2] Дэвенпорт Г., Мультипликативная теория чисел, пер. с англ., М., 1971; [3] Прахар К., Распределение простых чисел, пер. с нем., М., 1967; [4] Чудаков Н. Г., Введение в теории L-функций Дирихле, М.-Л., 1947; [5] WalfiszA., Weylsche Exponentialsummen in der neueren Zahlentheorie, В., 1963; [6] Монтгомери Г., Мультипликативная теория чисел, пер. с англ., 1974; [7] Лаврик А. Ф., "Матем. заметки", 1975, т. 17, в. 5, с. 809-17. А. Ф. Лаврик. |
|
|
|

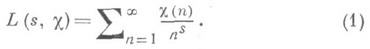
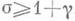 , g>0. Если c- неглавный характер, то
, g>0. Если c- неглавный характер, то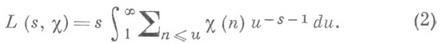
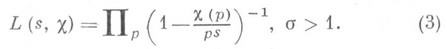
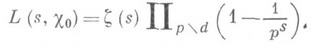
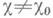 и c* -примитивный характер, к-рый индуцирует характер Xmod d, то
и c* -примитивный характер, к-рый индуцирует характер Xmod d, то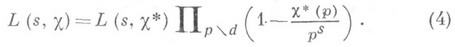
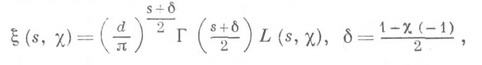
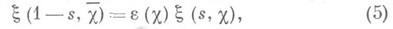
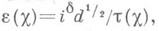 |e(c)|=1, t(c).- Гаусса сумма,c.- характер, комплексно сопряженный с c. Это равенство наз. функциональным уравнением функции L(s,c). Из него и формул (2) и (4) следует, что функции L(s,c), x(s, c). являются целыми функциями для всех
|e(c)|=1, t(c).- Гаусса сумма,c.- характер, комплексно сопряженный с c. Это равенство наз. функциональным уравнением функции L(s,c). Из него и формул (2) и (4) следует, что функции L(s,c), x(s, c). являются целыми функциями для всех 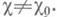 Причем, при
Причем, при 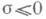 L(s, c) = 0 лишь в точках s=-2v-d, v=0, 1,2,..., и в точках s, где произведение из (4) обращается в нуль; эти точки наз. тривиальными нулями L(s,c). Остальные нули L(s, у )наз. нетривиальными нулями. Для s>1 функция
L(s, c) = 0 лишь в точках s=-2v-d, v=0, 1,2,..., и в точках s, где произведение из (4) обращается в нуль; эти точки наз. тривиальными нулями L(s,c). Остальные нули L(s, у )наз. нетривиальными нулями. Для s>1 функция 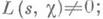 Ш. Ж. Валле Пуссен (Ch. J. Vallee-Poussin) показал, что
Ш. Ж. Валле Пуссен (Ch. J. Vallee-Poussin) показал, что 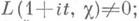 так что все нетривиальные нули Д. L-ф. лежат в области 0<s<1, к-рая наз. критической полосой.
так что все нетривиальные нули Д. L-ф. лежат в области 0<s<1, к-рая наз. критической полосой.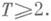 Тогда
Тогда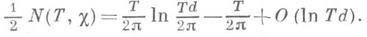
 - функция Мангольдта,
- функция Мангольдта,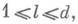 (l, d)=l,
(l, d)=l,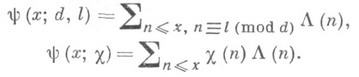

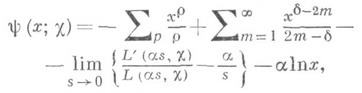
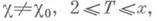
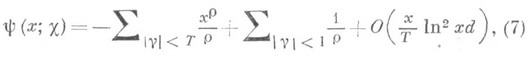
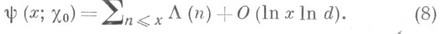
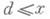
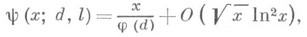
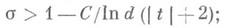 если же c - действительный неглавный характер mod d, то L(s,c) может иметь в этой области самое большое один простой действительный (t=0) нуль, к-рый наз. исключительным нулем L(s,c). Для исключительного нуля b, из формул числа классов квадратичных полей, выведено неравенство
если же c - действительный неглавный характер mod d, то L(s,c) может иметь в этой области самое большое один простой действительный (t=0) нуль, к-рый наз. исключительным нулем L(s,c). Для исключительного нуля b, из формул числа классов квадратичных полей, выведено неравенство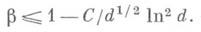
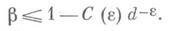
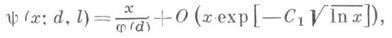 где С 1- абсолютная постоянная для
где С 1- абсолютная постоянная для 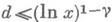 при нек-ром фиксировании g>0 и C1=C1(N)- "неэффективная" постоянная для
при нек-ром фиксировании g>0 и C1=C1(N)- "неэффективная" постоянная для 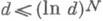 при любом фиксированном N>l-g.
при любом фиксированном N>l-g.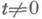 во многом аналогична теории дзета-функции Римана (см. [5]) и последняя граница нулей L(s,c), полученная по Виноградова методу оценки тригонометрич. сумм, имеет вид:
во многом аналогична теории дзета-функции Римана (см. [5]) и последняя граница нулей L(s,c), полученная по Виноградова методу оценки тригонометрич. сумм, имеет вид: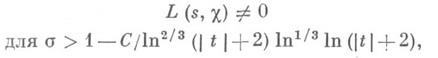
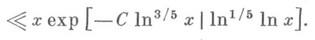
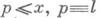 (mod d), с главным членом li x/j(d). вместо x/j(d). иостаточным членом, меньшим на множитель ln x.
(mod d), с главным членом li x/j(d). вместо x/j(d). иостаточным членом, меньшим на множитель ln x.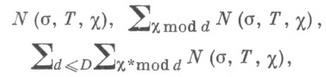
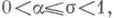 |t|<T, c*- примитивный характер mod d.
|t|<T, c*- примитивный характер mod d.