|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ДИРИХЛЕ РЯДЗначение ДИРИХЛЕ РЯД в математической энциклопедии: для аналитической почти периодической функции - ряд вида
представляющий собой все ряды Фурье аналитической регулярной почти периодической в полосе (a, b), Двум различным почти периодическим в одной и той же полосе функциям соответствуют два различных Д. р. В случае 2p-периодич. функции ряд (*) переходит в ряд Лорана. Числа А п и L п наз., соответственно, коэффициентами и показателями Дирихле. В отличие от классического Д. р. множество действительных показателей L п в (*) может иметь конечные предельные точки, и, даже, быть всюду плотным. Если все показатели Дирихле имеют один и тот же знак, напр., если f(s)- почти периодич. функция в полосе (а, Р) и в (*)
являются рядами Дирихле двух функций f1(s)и f2(s), почти периодических в любой полосе Лит.:[1] Бор Г., Почти периодические функции, пер. с нем., М.-Л., 1934; [2] Левитан Б. М., Почти периодические функции, М., 1953. Е. А. Бредихина. |
|
|
|


 , функции f(s)=f(t+it) на конти-. нуальной совокупности прямых R(s) = t (см. Почти периодическая функция аналитическая).
, функции f(s)=f(t+it) на конти-. нуальной совокупности прямых R(s) = t (см. Почти периодическая функция аналитическая). то f(s) - почти периодич. функция в полосе
то f(s) - почти периодич. функция в полосе  и
и  равномерно по t. Аналогичная теорема имеет место для положительных показателей Дирихле (см. [2]). Если f(s)- почти периодич. функция в полосе [a, b] и неопределенный интеграл функции f(s) в полосе [a, b] ограничен, то ряды
равномерно по t. Аналогичная теорема имеет место для положительных показателей Дирихле (см. [2]). Если f(s)- почти периодич. функция в полосе [a, b] и неопределенный интеграл функции f(s) в полосе [a, b] ограничен, то ряды
 соответственно
соответственно 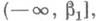 b1<b.
b1<b.