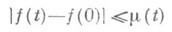|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ДИНИ ПРИЗНАКЗначение ДИНИ ПРИЗНАК в математической энциклопедии: если 2p-периодическая интегрируемая на отрезке [0, 2p] функция f(x)в точке х 0 удовлетворяет условию
при фиксированном числе S,
для малых t. Лит.:[1] Dini U., Serie di Fourier e altre rappresentazioni analitiche delle funzione di una variable reale, Pisa, 1880; [2] Зигмунд А., Тригонометрические ряды, пер. с англ., т. 1, М., 1965. Б. И. Голубое. |
|
|
|


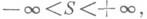 и каком-либо d>0, то ряд Фурье функции f(x)в точке х 0 сходится к числу S. Д. п. доказан У. Дини [1]. Его утверждение окончательно в следующем смысле. Если
и каком-либо d>0, то ряд Фурье функции f(x)в точке х 0 сходится к числу S. Д. п. доказан У. Дини [1]. Его утверждение окончательно в следующем смысле. Если  - такая непрерывная функция, что функция m(t)/t не интегрируема в окрестности точки 2=0, то можно найти непрерывную функцию f(t), ряд Фурье к-рой расходится в точке t=0, причем
- такая непрерывная функция, что функция m(t)/t не интегрируема в окрестности точки 2=0, то можно найти непрерывную функцию f(t), ряд Фурье к-рой расходится в точке t=0, причем