|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
АЛГОРИТМА СЛОЖНОСТЬЗначение АЛГОРИТМА СЛОЖНОСТЬ в математической энциклопедии: вычислений - функция, дающая числовую оценку трудности (громоздкости) процессов применения алгоритма к исходным данным. Уточнением А. с. вычислений служит понятие сигнализирующей функции (или просто сигнализирующей) - функции, к-рая задается разрешимым отношением между объектами применения алгоритма и натуральными числами и имеет область определения, совпадающую с областью применимости алгоритма. Чаще всего рассматриваются временные и пространственные характеристики алгоритмич. процессов. Так, для Тьюринга машины М сигнализирующая функция времени (время работы) Общей особенностью этих двух конкретных типов сигнализирующих является наличие эффективной процедуры, позволяющей для любого алгоритма Таким образом, последнее равенство объявляется эквивалентом высказывания "сложность вычисления Фиксируя ту или иную меру вычислений, можно ставить задачи о сложности вычисления конкретных функций f, напр, об отыскании алгоритма Другим важным направлением в теории сложности вычислений является изучение классов сложности - множеств функций, для к-рых существуют вычисления со сложностью, не превышающей к.-л. границы из множества границ, задающих класс. К этому направлению можно отнести и задачи сравнения сложности вычисления для различных типов алгоритмов (автоматов): переход к иной алгоритмич. системе и мере сложности обычно равносилен рассмотрению подходящей новой меры для исходной концепции алгоритмов. Укажем нек-рые фундаментальные результаты, не зависящие от выбора меры сложности (в том числе и от выбора конкретного уточнения понятия алгоритма) - лишь бы существовала, напр., эффективная возможность взаимного моделирования алгоритмов рассматриваемого типа и обыкновенных машин Тьюринга. (Для простоты можно представить себе дело так, что речь идет о времени вычисления на машинах Тьюринга натураль-нозначных функций натурального аргумента.) Пусть Ти hсуть вычислимые натуральнозначные функции (см. Вычислимая функция).на объектах применения алгоритмов, f - функция, определенная на тех же объектах и принимающая лишь два значения (например, 0 и 1). Во-первых, существуют сколь угодно сложно вычислимые функции. Точнее, для любой функции Тсуществует вычислимая функция неверно лишь в ограниченном числе случаев. Во-вторых, существуют функции, любое вычисление к-рых в принципе может быть улучшено как угодно сильно. Точнее, имеет место теорема ускорения: для любой функции в случае для почти всех Для мер вычислении, определяющих время работы и объем памяти, заключение теоремы ускорения верно для большинства вычислений в такой форме: если Установлено, что время распознавания равенства слов равно (по порядку) Сложностный подход оказывается полезным при изучении известных иерархий классов общерекурсивных функций, связанных с логическими и алгебраическими их особенностями. Так, напр., примитивно рекурсивные функции оказываются в точности теми функциями, к-рые вычислимы на машинах Тьюринга с объемом памяти, ограниченным определенной функцией. Факты существования достаточно сложно распознаваемых свойств, не зависящие от выбора вычислений, доказываются применением диагонального процесса. Их естественные аналоги были обнаружены для нек-рых разрешимых элементарных теорий и в областях, примыкающих к математич. лингвистике. В то же время для многих практически важных проблем получение хороших нижних границ сопряжено со значительными трудностями. Так, в частности, обстоит дело с задачами переборного характера, к-рые уточняются (в одном из вариантов) как задачи об отыскании среди слов определенной длины слова, удовлетворяющего вычислимому за полиномиальное время условию. Упомянем еще о сложности вычислений на недетерминированных автоматах и автоматах вероятностных. В первом случае речь идет о процессах с элементами произвола, и под сложностью вычислений понимается сложность "самого простого" варианта процесса. Во втором - конкретный ход процесса определяется, помимо программы и аргумента, последовательностью показаний датчика случайных чисел, а результат должен с большой вероятностью совпадать со значением вычисляемой функции. В обоих случаях удается доказать иногда уменьшение сложности вычислений по сравнению с детерминированными процессами. Качество алгоритмов оценивают не только с точки зрения А. с. вычислений, но и с точки зрения алгоритма сложности описания. Имеются результаты, совмещающие оба подхода. Лит.:[1] Хартманис Дж., Хопкрофт Д ж. Э., "Кибернетический сборник", 1974, вып. 11, с. 131-76. Н. В. Петри.
|
|
|
|

 есть число tтактов работы Мпри преобразовании исходных слои Рв заключительные; сигнализирующая памяти (или емкое т и)
есть число tтактов работы Мпри преобразовании исходных слои Рв заключительные; сигнализирующая памяти (или емкое т и)  определяется как количество ячеек ленты, в к-рых хотя бы раз побывала головка машины при работе над Р. Сходным образом определяются сигнализирующие времени и емкости для нормальных алгорифмов, итеративных сетей, многоголо-вочиых и многоленточных машин Тьюринга и т. п.
определяется как количество ячеек ленты, в к-рых хотя бы раз побывала головка машины при работе над Р. Сходным образом определяются сигнализирующие времени и емкости для нормальных алгорифмов, итеративных сетей, многоголо-вочиых и многоленточных машин Тьюринга и т. п. (т. е., в частности, для машины Тьюринга, или, точнее, для ее программы), всякого исходного данного хи натурального числа tустановить, верно ли, что процесс применения
(т. е., в частности, для машины Тьюринга, или, точнее, для ее программы), всякого исходного данного хи натурального числа tустановить, верно ли, что процесс применения  к хзаканчивается со сложностью t. Это обстоятельство положено в основу аксиоматич. построения теории сложности вычислений (см. [1]). Эффективная процедура г наз. мерой вычислений, если она: 1) всегда заканчивается результатом 0 или 1 применительно к тройкам вида (алгоритм, исходное данное, натуральное число), 2) обладает тем свойством, что для любого алгоритма
к хзаканчивается со сложностью t. Это обстоятельство положено в основу аксиоматич. построения теории сложности вычислений (см. [1]). Эффективная процедура г наз. мерой вычислений, если она: 1) всегда заканчивается результатом 0 или 1 применительно к тройкам вида (алгоритм, исходное данное, натуральное число), 2) обладает тем свойством, что для любого алгоритма  и исходного данного хравенство
и исходного данного хравенство  верно не более чем при одном натуральном t, причем такое tсуществует тогда и только тогда, когда процесс применения a к хзаканчивается. Вводится сигнализирующая функция
верно не более чем при одном натуральном t, причем такое tсуществует тогда и только тогда, когда процесс применения a к хзаканчивается. Вводится сигнализирующая функция  по мере r для
по мере r для  ':
':  тогда и только тогда, когда
тогда и только тогда, когда 
 на хравна t(по мере r)".
на хравна t(по мере r)". , вычисляющего f "лучше других алгоритмов". Однако, как показывает теорема ускорения (см. ниже), подобная постановка не всегда правомерна, и речь может идти скорее об описании скорости роста тех сигнализирующих
, вычисляющего f "лучше других алгоритмов". Однако, как показывает теорема ускорения (см. ниже), подобная постановка не всегда правомерна, и речь может идти скорее об описании скорости роста тех сигнализирующих  , для к-рых
, для к-рых  вычисляет f [напр., об отыскании верхней и нижней границ сложности вычисления f - двух функций
вычисляет f [напр., об отыскании верхней и нижней границ сложности вычисления f - двух функций  таких, что существует вычисление
таких, что существует вычисление  функции f, для к-рого
функции f, для к-рого  , и для всякого алгоритма
, и для всякого алгоритма  , вычисляющего f, функция
, вычисляющего f, функция  в каком-то смысле мажорирует g].
в каком-то смысле мажорирует g]. такая, что для всякого алгоритма
такая, что для всякого алгоритма  , вычисляющего
, вычисляющего  , неравенство
, неравенство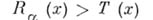
 (напр.,
(напр., 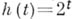 ) можно указать вычислимую функцию
) можно указать вычислимую функцию  такую, что для всякого алгоритма
такую, что для всякого алгоритма  , вычисляющего
, вычисляющего  , не может не найтись (здесь эффективная процедура не предполагается) алгоритм
, не может не найтись (здесь эффективная процедура не предполагается) алгоритм  , тоже вычисляющий
, тоже вычисляющий  и такой, что для всех х(кроме конечного множества)
и такой, что для всех х(кроме конечного множества)
 это приводит к
это приводит к 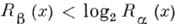
 .
. вычислима со сложностью
вычислима со сложностью  , то она вычислима и со сложностью
, то она вычислима и со сложностью  (говорят, что
(говорят, что  вычислима со сложностью
вычислима со сложностью  , если для нек-рого
, если для нек-рого  , вычисляющего ее,
, вычисляющего ее,  для всех слов Рдлины и в рассматриваемом алфавите). Поэтому временная и объемная сложности вычислений конкретных функций часто оцениваются с точностью до порядка. Ниже приведены нек-рые конкретные результаты.
для всех слов Рдлины и в рассматриваемом алфавите). Поэтому временная и объемная сложности вычислений конкретных функций часто оцениваются с точностью до порядка. Ниже приведены нек-рые конкретные результаты.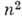 для машин Тьюринга и нормальных алгорифмов; что всякое свойство слов, распознаваемое на машинах Тьюринга за время, по порядку меньшее функции
для машин Тьюринга и нормальных алгорифмов; что всякое свойство слов, распознаваемое на машинах Тьюринга за время, по порядку меньшее функции  распознается и за время п;что вычисления на машинах Тьюринга со временем
распознается и за время п;что вычисления на машинах Тьюринга со временем  (для
(для  по порядку) моделируются на машинах Тьюринга с объемом памяти
по порядку) моделируются на машинах Тьюринга с объемом памяти  Доказано, что умножение двух n- разрядных чисел на многоленточных машинах Тьюринга осуществимо за время
Доказано, что умножение двух n- разрядных чисел на многоленточных машинах Тьюринга осуществимо за время  , но всегда более ппо порядку, а итеративные сети могут умножать в реальное время, т. е. i-й младший разряд произведения появляется на выходе с подачей на вход i-х разрядов сомножителей. При моделировании алгоритмич. процессов одного типа с помощью других сложность вычислений, вообще говоря, меняется. Так, уменьшение размерности итеративных сетей приводит к увеличению времени. В то же время замена многоголовочных машин Тьюринга многоленточными не меняет времени вычисления функций. Для многих типов алгоритмов доказывается возможность их моделирования на машинах Тьюринга с полиномиальным (обычно даже квадратичным) возрастанием времени работы и незначительным увеличением объема памяти.
, но всегда более ппо порядку, а итеративные сети могут умножать в реальное время, т. е. i-й младший разряд произведения появляется на выходе с подачей на вход i-х разрядов сомножителей. При моделировании алгоритмич. процессов одного типа с помощью других сложность вычислений, вообще говоря, меняется. Так, уменьшение размерности итеративных сетей приводит к увеличению времени. В то же время замена многоголовочных машин Тьюринга многоленточными не меняет времени вычисления функций. Для многих типов алгоритмов доказывается возможность их моделирования на машинах Тьюринга с полиномиальным (обычно даже квадратичным) возрастанием времени работы и незначительным увеличением объема памяти.