|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ДИКСОНА ИНВАРИАНТЗначение ДИКСОНА ИНВАРИАНТ в математической энциклопедии: - конструкция, используемая при изучении квадратичных форм над полями характеристики 2, позволяющая, в частности, вводить аналоги специальной ортогональной группы над такими полями. А именно, Д. и. есть элемент D(u)произвольного поля кхарактеристики 2, сопоставляемый всякому подобию и четномерного векторного пространства Енад kотносительно симметрической билинейной формы f, ассоциированной с невырожденной квадратичной формой Qна Е. Д. и. введен Л. Диксоном [1]. В силу условия на характеристику поля форма f является знакопеременной, и в E существует базис el, ..., e2s, для к-рого
при
для любых векторов хи у из Е, и пусть для каждого i=i,. .., s
Тогда элемент из квида
наз. инвариантом Диксона подобия и относительно базиса e1, . . ., e.2s. Для того чтобы ибыло подобием относительно Qс коэффициентом подобия а(и){т. е. Q(u(x))=a(u)Q(х). для любого вектора Если Q1- форма, определяемая равенством Q1(x)=Q(u(x))для любого вектора
Лит.:[1] Dickson L. E., Linear Groups..., Lpz., 1901; [2] Бурбаки Н., Алгебра. Модули, кольца, формы, пер. с франц., М., 1966; [3] Дьедонне Ж., Геометрия классических групп, пер. с франц., М., 1974. В. Л. Попов. |
|
|
|


 (см. Витта разложение). Пусть
(см. Витта разложение). Пусть
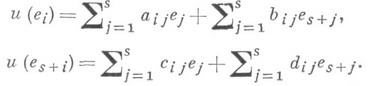

 , необходимо и достаточно, чтобы D(u)=0 или D(u) - a(u). Подобия иотносительно Q, для к-рых D(u) = 0, наз. прямыми подобиями. Прямые подобия образуют в группе всех подобий относительно Qнормальный делитель индекса 2.
, необходимо и достаточно, чтобы D(u)=0 или D(u) - a(u). Подобия иотносительно Q, для к-рых D(u) = 0, наз. прямыми подобиями. Прямые подобия образуют в группе всех подобий относительно Qнормальный делитель индекса 2. а D(Q) и D(Q1) -псевдодискриминанты этих форм относительно базиса е 1, . .., e2s, т. е.
а D(Q) и D(Q1) -псевдодискриминанты этих форм относительно базиса е 1, . .., e2s, т. е.
