"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ДИКОЕ ВЛОЖЕНИЕЗначение ДИКОЕ ВЛОЖЕНИЕ в математической энциклопедии:
топологического пространства Xв топологическое пространство Y- вложение, к-рое топологически не эквивалентно вложению из нек-рого класса выделенных вложений, наз. правильными, или ручными, вложениями. Наиболее употребительными являются следующие случаи; в качестве Yв них берется n-мерное евклидово пространство Rn. 1) Пусть Месть k-мерное топологич. многообразие. Топологич. вложение g: наз. диким, если не существует гомеоморфизма Rn на себя, переводящего g(M)в локально плоское подмногообразие Rn. наз. диким, если не существует гомеоморфизма Rn на себя, переводящего g(M)в локально плоское подмногообразие Rn. 2) Пусть Ресть k-мерный полиэдр. Топологич. вложение g: наз. диким, если не существует гомеоморфизма Rn на себя, переводящего g(P)в полиэдр (т. е. в тело нек-рой триангуляции) Rn. наз. диким, если не существует гомеоморфизма Rn на себя, переводящего g(P)в полиэдр (т. е. в тело нек-рой триангуляции) Rn. 3) Пусть Кесть k-мерное локально компактное пространство. Топологич. вложение g:  наз. диким, если не существует гомеоморфизма Rn на себя, переводящего g{K )в подмножество k-мерного Менгера компакта наз. диким, если не существует гомеоморфизма Rn на себя, переводящего g{K )в подмножество k-мерного Менгера компакта  Если размерность  и и  то введенные свойства во всех трех случаях характеризуются локально гомотопич. свойством: вложение является диким тогда и только тогда, когда g(X)не удовлетворяет свойству 1-ULC (см. Топология вложений). Положение вещей для коразмерностей п-k=1. и 2 значительно сложнее: вопрос решен здесь для многообразий коразмерности 1 при то введенные свойства во всех трех случаях характеризуются локально гомотопич. свойством: вложение является диким тогда и только тогда, когда g(X)не удовлетворяет свойству 1-ULC (см. Топология вложений). Положение вещей для коразмерностей п-k=1. и 2 значительно сложнее: вопрос решен здесь для многообразий коразмерности 1 при 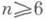 и не решен полностью для вложений коразмерности 2 как для многообразий, так и для полиэдров. Все сказанное имеет смысл и тогда, когда в качестве Yберется n-мерное многообразие, топологическое или кусочно линейное. М. А. Штанько. и не решен полностью для вложений коразмерности 2 как для многообразий, так и для полиэдров. Все сказанное имеет смысл и тогда, когда в качестве Yберется n-мерное многообразие, топологическое или кусочно линейное. М. А. Штанько.
|

 наз. диким, если не существует гомеоморфизма Rn на себя, переводящего g(M)в локально плоское подмногообразие Rn.
наз. диким, если не существует гомеоморфизма Rn на себя, переводящего g(M)в локально плоское подмногообразие Rn. наз. диким, если не существует гомеоморфизма Rn на себя, переводящего g(P)в полиэдр (т. е. в тело нек-рой триангуляции) Rn.
наз. диким, если не существует гомеоморфизма Rn на себя, переводящего g(P)в полиэдр (т. е. в тело нек-рой триангуляции) Rn. наз. диким, если не существует гомеоморфизма Rn на себя, переводящего g{K )в подмножество k-мерного Менгера компакта
наз. диким, если не существует гомеоморфизма Rn на себя, переводящего g{K )в подмножество k-мерного Менгера компакта 
 и
и  то введенные свойства во всех трех случаях характеризуются локально гомотопич. свойством: вложение является диким тогда и только тогда, когда g(X)не удовлетворяет свойству 1-ULC (см. Топология вложений). Положение вещей для коразмерностей п-k=1. и 2 значительно сложнее: вопрос решен здесь для многообразий коразмерности 1 при
то введенные свойства во всех трех случаях характеризуются локально гомотопич. свойством: вложение является диким тогда и только тогда, когда g(X)не удовлетворяет свойству 1-ULC (см. Топология вложений). Положение вещей для коразмерностей п-k=1. и 2 значительно сложнее: вопрос решен здесь для многообразий коразмерности 1 при 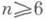 и не решен полностью для вложений коразмерности 2 как для многообразий, так и для полиэдров. Все сказанное имеет смысл и тогда, когда в качестве Yберется n-мерное многообразие, топологическое или кусочно линейное. М. А. Штанько.
и не решен полностью для вложений коразмерности 2 как для многообразий, так и для полиэдров. Все сказанное имеет смысл и тогда, когда в качестве Yберется n-мерное многообразие, топологическое или кусочно линейное. М. А. Штанько.