"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
АЛГОРИТМ ЛОКАЛЬНЫЙ
Значение АЛГОРИТМ ЛОКАЛЬНЫЙ в математической энциклопедии:
алгоритм, устанавливающий свойства элементов множества и использующий на каждом шаге при этом только информацию об окрестности элемента. В терминах А. л. естественно формулируются и решаются задачи о существовании или несуществовании эффективных алгоритмов для различных дискретных экстремальных задач.
Пусть задано семейство  множеств, и пусть каждой паре
множеств, и пусть каждой паре  , где
, где  , сопоставлено множество
, сопоставлено множество 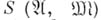 такое, что: 1)
такое, что: 1)  , 2)
, 2)  ,3) если
,3) если 
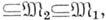 то
то  . Тогда множество
. Тогда множество 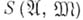 наз. окрестностью
наз. окрестностью  . Примерами окрестностей служат окрестности конъюнкции в сокращенной нормальной форме (см. Булевых функций минимизация).
. Примерами окрестностей служат окрестности конъюнкции в сокращенной нормальной форме (см. Булевых функций минимизация).
Пусть Г - конечный неориентированный граф,
 - множество вершин Г,
- множество вершин Г,  - множество ребер Г. Окрестность
- множество ребер Г. Окрестность 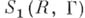 'ребра
'ребра  графа Г состоит из всех вершин ребер, инцидентных ребру R, а также из всех ребер, вершины к-рых входят в окрестность
графа Г состоит из всех вершин ребер, инцидентных ребру R, а также из всех ребер, вершины к-рых входят в окрестность  I. Пусть определена окрестность
I. Пусть определена окрестность  , тогда окрестность
, тогда окрестность  состоит из всех вершин ребер, инцидентных вершинам окрестности
состоит из всех вершин ребер, инцидентных вершинам окрестности  и всех ребер, вершины к-рых принадлежат окрестности
и всех ребер, вершины к-рых принадлежат окрестности  . Аналогично вводятся окрестности
. Аналогично вводятся окрестности  для произвольной вершины
для произвольной вершины  графа Г.
графа Г.
Пусть на парах  определена система двуместных предикатов
определена система двуместных предикатов  к-рая разбита на два непересекающихся подмножества
к-рая разбита на два непересекающихся подмножества 
 . Элементы первого подмножества наз. основными предикатами, второго - вспомогательными предикатами. Вектор
. Элементы первого подмножества наз. основными предикатами, второго - вспомогательными предикатами. Вектор  наз. информационным, если
наз. информационным, если  . Вектор
. Вектор  наз. д о-пустимым для
наз. д о-пустимым для  " ...., если для всех
" ...., если для всех  выполнено равенство
выполнено равенство  . Множество
. Множество  всех информационных векторов, допустимых для А. в
всех информационных векторов, допустимых для А. в  , наз. информационным множеством
, наз. информационным множеством  в
в 
Пусть  и
и  , i= =1, 2, ..., q. Множество
, i= =1, 2, ..., q. Множество  наз. допустимым для
наз. допустимым для  . Класс
. Класс  всех допустимых для
всех допустимых для  множеств
множеств  наз. информационным классом множества
наз. информационным классом множества  по системе предикатов
по системе предикатов  Очевидно, что окрестность
Очевидно, что окрестность  определяет окрестность
определяет окрестность 
Введем систему функций 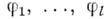 таких, что
таких, что  Функции
Функции  определены на всех парах
определены на всех парах  таких, что
таких, что  и удовлетворяют следующим условиям: 1)
и удовлетворяют следующим условиям: 1)  ; 2) множество
; 2) множество  , которое получается из
, которое получается из  заменой элемента
заменой элемента  , допустимо для
, допустимо для  , т. е.
, т. е. 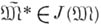 . Для краткости пары
. Для краткости пары 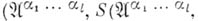
 обозначаются через
обозначаются через  .
.
На нек-рых из описанных множеств вводится частичный порядок: 1) на множестве 
 2) на множестве
2) на множестве  информационных векторов длины
информационных векторов длины  , если
, если 
 3) на множестве элементов с отметками -
3) на множестве элементов с отметками -  . , если
. , если 
 4) на множестве
4) на множестве 
 , если, во-первых,
, если, во-первых,  принадлежат одному информационному классу
принадлежат одному информационному классу  и, во-вторых, из того, что
и, во-вторых, из того, что  и
и  , следует
, следует  ; 5) на множестве окрестностей вида
; 5) на множестве окрестностей вида 
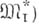 и
и  , тогда и только тогда, когда
, тогда и только тогда, когда  и из условий
и из условий 
 следует, что
следует, что 
Пусть Аи В - элементы одного из множеств 1) - 5). Если  то элементы Аи Вназ. равными по информации, что обозначается
то элементы Аи Вназ. равными по информации, что обозначается  Функция
Функция  наз. монотонной, если из соотношения
наз. монотонной, если из соотношения  следует, что для i= 1, 2, ..., l
следует, что для i= 1, 2, ..., l 
Для определения А. л. необходимо также ввести алгоритм 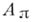 упорядочивания. Пусть М- произвольное множество, составленное из элементов с информационными векторами, а
упорядочивания. Пусть М- произвольное множество, составленное из элементов с информационными векторами, а 
Рассмотрим множество  всех пар
всех пар  таких, что
таких, что  Алгоритм А л упорядочивает множество
Алгоритм А л упорядочивает множество 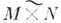 . А. л. Аполностью определяется системой предикатов
. А. л. Аполностью определяется системой предикатов  разбиением этой системы на основные
разбиением этой системы на основные  и вспомогательные
и вспомогательные  предикаты, системой монотонных функций
предикаты, системой монотонных функций  и алгоритмом
и алгоритмом  .
.
Пусть  . Первый шаг А. л. состоит в следующем. К множеству
. Первый шаг А. л. состоит в следующем. К множеству  , где
, где  , применяется алгоритм
, применяется алгоритм  ; длк первой по порядку пары
; длк первой по порядку пары  вычисляется
вычисляется 
 и элемент
и элемент  заменяется на
заменяется на  если
если  то берется вторая пара, и т. д.; если для всех элементов
то берется вторая пара, и т. д.; если для всех элементов  выполнено равенство
выполнено равенство 
 то А. л. Азаканчивается после просмотра всех пар из
то А. л. Азаканчивается после просмотра всех пар из  . В противном случае, после замены вектора
. В противном случае, после замены вектора 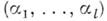 на новый вектор
на новый вектор  если нет больше элементов, у к-рых на первых rместах в информационных векторах имеется хотя бы один символ Д, алгоритм Азаканчивается; если они есть, то заканчивается первый шаг А. л. Пусть выполнено nшагов А. л. А. Описание
если нет больше элементов, у к-рых на первых rместах в информационных векторах имеется хотя бы один символ Д, алгоритм Азаканчивается; если они есть, то заканчивается первый шаг А. л. Пусть выполнено nшагов А. л. А. Описание  шага в точности повторяет описание первого, если вместо множества
шага в точности повторяет описание первого, если вместо множества  рассматривать множество
рассматривать множество  в к-рое перешло
в к-рое перешло 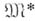 после первых пшагов А. я. А. В силу монотонности функций
после первых пшагов А. я. А. В силу монотонности функций  ,
,
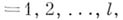 А. л. Азакончится после конечного числа шагов.
А. л. Азакончится после конечного числа шагов.
Исходными теоремами для А. л. являются теорема единственности и теорема существования наилучшего алгоритма. Первая теорема утверждает, что результат вычислений основных предикатов не зависит от алгоритма  (порядка обхода элементов множества
(порядка обхода элементов множества  ). Вторая теорема утверждает существование в весьма общих предположениях наилучшего А. л., т. е. А. л., к-рый по заданной фиксированной системе окрестностей вычисляет заданные основные предикаты при фиксированных вспомогательных предикатах всегда, когда это делает любой другой А. л. с той же системой окрестностей, основных и вспомогательных предикатов.
). Вторая теорема утверждает существование в весьма общих предположениях наилучшего А. л., т. е. А. л., к-рый по заданной фиксированной системе окрестностей вычисляет заданные основные предикаты при фиксированных вспомогательных предикатах всегда, когда это делает любой другой А. л. с той же системой окрестностей, основных и вспомогательных предикатов.
Задача получения наилучшего А. л. в явной форме решена для алгоритмов синтеза минимальных покрытий. Пусть задан набор  , где
, где  - множество,
- множество,  - сложность
- сложность 
 Сложность набора
Сложность набора  есть Требуется построить покрытие М множествами
есть Требуется построить покрытие М множествами  из числа
из числа  с минимальной сложностью. Система окрестностей
с минимальной сложностью. Система окрестностей  для каждого
для каждого  вводится аналогично системе окрестностей для конъюнкций. Наилучший А. л. строится для системы окрестностей
вводится аналогично системе окрестностей для конъюнкций. Наилучший А. л. строится для системы окрестностей  при фиксированных предикатах: множество вспомогательных предикатов пусто; в качестве основных рассматриваются предикаты
при фиксированных предикатах: множество вспомогательных предикатов пусто; в качестве основных рассматриваются предикаты  ("
(" не входит ни в одно минимальное покрытие М").и Р г
не входит ни в одно минимальное покрытие М").и Р г .("
.(" входит во все минимальные покрытия М"). Наилучшие А. л. построены также для вычисления простых свойств ребер графа. Большое число различных А. л. было предложено для решения задач минимизации булевых функций, дискретного линейного программирования и т. д.
входит во все минимальные покрытия М"). Наилучшие А. л. построены также для вычисления простых свойств ребер графа. Большое число различных А. л. было предложено для решения задач минимизации булевых функций, дискретного линейного программирования и т. д.
Важное место в теории А. л. занимают задачи о невычислимости экстремальных свойств в классе А. л. Если на парах  , задана система вложенных окрестностей:
, задана система вложенных окрестностей:
 и А. л. работает по системе окрестностей
и А. л. работает по системе окрестностей  где
где 
 , то говорят, что А. л. имеет индекс k. Число предикатов
, то говорят, что А. л. имеет индекс k. Число предикатов  в определении А. л. естественно считать величиной па мят и А. л. Пусть задано множество
в определении А. л. естественно считать величиной па мят и А. л. Пусть задано множество  предикатов
предикатов  Считается, что все предикаты, участвующие в определении А. л., принадлежат
Считается, что все предикаты, участвующие в определении А. л., принадлежат  . Пусть
. Пусть  - результат применения А. л. А к
- результат применения А. л. А к . Про предикат
. Про предикат  говорят, что он не является
говорят, что он не является  -вычислимым, если для всякого А. л. индекса kс величиной памяти l, основным предикатом
-вычислимым, если для всякого А. л. индекса kс величиной памяти l, основным предикатом 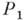 и вспомогательными
и вспомогательными  из
из  найдется множество
найдется множество  такое, что в
такое, что в  предикат
предикат  будет вычислен не для всех элементов.
будет вычислен не для всех элементов.
Пусть  - совокупность всех булевых функций от переменных
- совокупность всех булевых функций от переменных  и
и  - предикат "конъюнкция
- предикат "конъюнкция  входит хотя бы в одну минимальную дизъюнктивную нормальную форму". При естественных ограничениях на класс предикатов
входит хотя бы в одну минимальную дизъюнктивную нормальную форму". При естественных ограничениях на класс предикатов  установлено, что предикат
установлено, что предикат 
не является  -вычислимым, если
-вычислимым, если  . Интересно отметить, что предикат
. Интересно отметить, что предикат  ) "конъюнкция
) "конъюнкция  входит хотя бы в одну тупиковую дизъюнктивную нормальную форму f" (см. Булевых функций нормальные формы).является (2, 1)-вычислимым, но не (1, 1)-вычислимым. Аналогичные результаты получены для предикатов, описывающих вхождение ребра в минимальный путь между заданными вершинами графа.
входит хотя бы в одну тупиковую дизъюнктивную нормальную форму f" (см. Булевых функций нормальные формы).является (2, 1)-вычислимым, но не (1, 1)-вычислимым. Аналогичные результаты получены для предикатов, описывающих вхождение ребра в минимальный путь между заданными вершинами графа.
Лит.:[1] Журавлев Ю. И., "Кибернетика", 1965, № 1, с. 12-19; 1966, №2, с. 1 - 11; [2] Хуторянская И. В., "Кибернетика", 1971, J* 1, с. 29-33; [3] Журавлев Ю. И., сб. "Проблемы кибернетики", 1962, вып. 8, с. 5-44.
См. также лит. при статье Булевых функций минимизация.
Ю. И. Журавлев.

 множеств, и пусть каждой паре
множеств, и пусть каждой паре  , где
, где  , сопоставлено множество
, сопоставлено множество 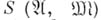 такое, что: 1)
такое, что: 1)  , 2)
, 2)  ,3) если
,3) если 
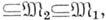 то
то  . Тогда множество
. Тогда множество 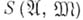 наз. окрестностью
наз. окрестностью  . Примерами окрестностей служат окрестности конъюнкции в сокращенной нормальной форме (см. Булевых функций минимизация).
. Примерами окрестностей служат окрестности конъюнкции в сокращенной нормальной форме (см. Булевых функций минимизация).
 - множество вершин Г,
- множество вершин Г,  - множество ребер Г. Окрестность
- множество ребер Г. Окрестность 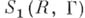 'ребра
'ребра  графа Г состоит из всех вершин ребер, инцидентных ребру R, а также из всех ребер, вершины к-рых входят в окрестность
графа Г состоит из всех вершин ребер, инцидентных ребру R, а также из всех ребер, вершины к-рых входят в окрестность  I. Пусть определена окрестность
I. Пусть определена окрестность  , тогда окрестность
, тогда окрестность  состоит из всех вершин ребер, инцидентных вершинам окрестности
состоит из всех вершин ребер, инцидентных вершинам окрестности  и всех ребер, вершины к-рых принадлежат окрестности
и всех ребер, вершины к-рых принадлежат окрестности  . Аналогично вводятся окрестности
. Аналогично вводятся окрестности  для произвольной вершины
для произвольной вершины  графа Г.
графа Г. определена система двуместных предикатов
определена система двуместных предикатов  к-рая разбита на два непересекающихся подмножества
к-рая разбита на два непересекающихся подмножества 
 . Элементы первого подмножества наз. основными предикатами, второго - вспомогательными предикатами. Вектор
. Элементы первого подмножества наз. основными предикатами, второго - вспомогательными предикатами. Вектор  наз. информационным, если
наз. информационным, если  . Вектор
. Вектор  наз. д о-пустимым для
наз. д о-пустимым для  " ...., если для всех
" ...., если для всех  выполнено равенство
выполнено равенство  . Множество
. Множество  всех информационных векторов, допустимых для А. в
всех информационных векторов, допустимых для А. в  , наз. информационным множеством
, наз. информационным множеством  в
в 
 и
и  , i= =1, 2, ..., q. Множество
, i= =1, 2, ..., q. Множество  наз. допустимым для
наз. допустимым для  . Класс
. Класс  всех допустимых для
всех допустимых для  множеств
множеств  наз. информационным классом множества
наз. информационным классом множества  по системе предикатов
по системе предикатов  Очевидно, что окрестность
Очевидно, что окрестность  определяет окрестность
определяет окрестность 
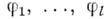 таких, что
таких, что  Функции
Функции  определены на всех парах
определены на всех парах  таких, что
таких, что  и удовлетворяют следующим условиям: 1)
и удовлетворяют следующим условиям: 1)  ; 2) множество
; 2) множество  , которое получается из
, которое получается из  заменой элемента
заменой элемента  , допустимо для
, допустимо для  , т. е.
, т. е. 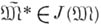 . Для краткости пары
. Для краткости пары 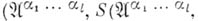
 обозначаются через
обозначаются через  .
.
 2) на множестве
2) на множестве  информационных векторов длины
информационных векторов длины  , если
, если 
 3) на множестве элементов с отметками -
3) на множестве элементов с отметками -  . , если
. , если 
 4) на множестве
4) на множестве 
 , если, во-первых,
, если, во-первых,  принадлежат одному информационному классу
принадлежат одному информационному классу  и, во-вторых, из того, что
и, во-вторых, из того, что  и
и  , следует
, следует  ; 5) на множестве окрестностей вида
; 5) на множестве окрестностей вида 
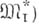 и
и  , тогда и только тогда, когда
, тогда и только тогда, когда  и из условий
и из условий 
 следует, что
следует, что 
 то элементы Аи Вназ. равными по информации, что обозначается
то элементы Аи Вназ. равными по информации, что обозначается  Функция
Функция  наз. монотонной, если из соотношения
наз. монотонной, если из соотношения  следует, что для i= 1, 2, ..., l
следует, что для i= 1, 2, ..., l 
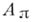 упорядочивания. Пусть М- произвольное множество, составленное из элементов с информационными векторами, а
упорядочивания. Пусть М- произвольное множество, составленное из элементов с информационными векторами, а 
 всех пар
всех пар  таких, что
таких, что  Алгоритм А л упорядочивает множество
Алгоритм А л упорядочивает множество 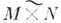 . А. л. Аполностью определяется системой предикатов
. А. л. Аполностью определяется системой предикатов  разбиением этой системы на основные
разбиением этой системы на основные  и вспомогательные
и вспомогательные  предикаты, системой монотонных функций
предикаты, системой монотонных функций  и алгоритмом
и алгоритмом  .
. . Первый шаг А. л. состоит в следующем. К множеству
. Первый шаг А. л. состоит в следующем. К множеству  , где
, где  , применяется алгоритм
, применяется алгоритм  ; длк первой по порядку пары
; длк первой по порядку пары  вычисляется
вычисляется 
 и элемент
и элемент  заменяется на
заменяется на  если
если  то берется вторая пара, и т. д.; если для всех элементов
то берется вторая пара, и т. д.; если для всех элементов  выполнено равенство
выполнено равенство 
 то А. л. Азаканчивается после просмотра всех пар из
то А. л. Азаканчивается после просмотра всех пар из  . В противном случае, после замены вектора
. В противном случае, после замены вектора 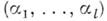 на новый вектор
на новый вектор  если нет больше элементов, у к-рых на первых rместах в информационных векторах имеется хотя бы один символ Д, алгоритм Азаканчивается; если они есть, то заканчивается первый шаг А. л. Пусть выполнено nшагов А. л. А. Описание
если нет больше элементов, у к-рых на первых rместах в информационных векторах имеется хотя бы один символ Д, алгоритм Азаканчивается; если они есть, то заканчивается первый шаг А. л. Пусть выполнено nшагов А. л. А. Описание  шага в точности повторяет описание первого, если вместо множества
шага в точности повторяет описание первого, если вместо множества  рассматривать множество
рассматривать множество  в к-рое перешло
в к-рое перешло 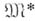 после первых пшагов А. я. А. В силу монотонности функций
после первых пшагов А. я. А. В силу монотонности функций  ,
,
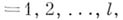 А. л. Азакончится после конечного числа шагов.
А. л. Азакончится после конечного числа шагов. (порядка обхода элементов множества
(порядка обхода элементов множества  ). Вторая теорема утверждает существование в весьма общих предположениях наилучшего А. л., т. е. А. л., к-рый по заданной фиксированной системе окрестностей вычисляет заданные основные предикаты при фиксированных вспомогательных предикатах всегда, когда это делает любой другой А. л. с той же системой окрестностей, основных и вспомогательных предикатов.
). Вторая теорема утверждает существование в весьма общих предположениях наилучшего А. л., т. е. А. л., к-рый по заданной фиксированной системе окрестностей вычисляет заданные основные предикаты при фиксированных вспомогательных предикатах всегда, когда это делает любой другой А. л. с той же системой окрестностей, основных и вспомогательных предикатов. , где
, где  - множество,
- множество,  - сложность
- сложность 
 Сложность набора
Сложность набора  есть Требуется построить покрытие М множествами
есть Требуется построить покрытие М множествами  из числа
из числа  с минимальной сложностью. Система окрестностей
с минимальной сложностью. Система окрестностей  для каждого
для каждого  вводится аналогично системе окрестностей для конъюнкций. Наилучший А. л. строится для системы окрестностей
вводится аналогично системе окрестностей для конъюнкций. Наилучший А. л. строится для системы окрестностей  при фиксированных предикатах: множество вспомогательных предикатов пусто; в качестве основных рассматриваются предикаты
при фиксированных предикатах: множество вспомогательных предикатов пусто; в качестве основных рассматриваются предикаты  ("
(" не входит ни в одно минимальное покрытие М").и Р г
не входит ни в одно минимальное покрытие М").и Р г .("
.(" входит во все минимальные покрытия М"). Наилучшие А. л. построены также для вычисления простых свойств ребер графа. Большое число различных А. л. было предложено для решения задач минимизации булевых функций, дискретного линейного программирования и т. д.
входит во все минимальные покрытия М"). Наилучшие А. л. построены также для вычисления простых свойств ребер графа. Большое число различных А. л. было предложено для решения задач минимизации булевых функций, дискретного линейного программирования и т. д. , задана система вложенных окрестностей:
, задана система вложенных окрестностей:
 и А. л. работает по системе окрестностей
и А. л. работает по системе окрестностей  где
где 
 , то говорят, что А. л. имеет индекс k. Число предикатов
, то говорят, что А. л. имеет индекс k. Число предикатов  в определении А. л. естественно считать величиной па мят и А. л. Пусть задано множество
в определении А. л. естественно считать величиной па мят и А. л. Пусть задано множество  предикатов
предикатов  Считается, что все предикаты, участвующие в определении А. л., принадлежат
Считается, что все предикаты, участвующие в определении А. л., принадлежат  . Пусть
. Пусть  - результат применения А. л. А к
- результат применения А. л. А к . Про предикат
. Про предикат  говорят, что он не является
говорят, что он не является  -вычислимым, если для всякого А. л. индекса kс величиной памяти l, основным предикатом
-вычислимым, если для всякого А. л. индекса kс величиной памяти l, основным предикатом 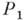 и вспомогательными
и вспомогательными  из
из  найдется множество
найдется множество  такое, что в
такое, что в  предикат
предикат  будет вычислен не для всех элементов.
будет вычислен не для всех элементов. - совокупность всех булевых функций от переменных
- совокупность всех булевых функций от переменных  и
и  - предикат "конъюнкция
- предикат "конъюнкция  входит хотя бы в одну минимальную дизъюнктивную нормальную форму". При естественных ограничениях на класс предикатов
входит хотя бы в одну минимальную дизъюнктивную нормальную форму". При естественных ограничениях на класс предикатов  установлено, что предикат
установлено, что предикат 
 -вычислимым, если
-вычислимым, если  . Интересно отметить, что предикат
. Интересно отметить, что предикат  ) "конъюнкция
) "конъюнкция  входит хотя бы в одну тупиковую дизъюнктивную нормальную форму f" (см. Булевых функций нормальные формы).является (2, 1)-вычислимым, но не (1, 1)-вычислимым. Аналогичные результаты получены для предикатов, описывающих вхождение ребра в минимальный путь между заданными вершинами графа.
входит хотя бы в одну тупиковую дизъюнктивную нормальную форму f" (см. Булевых функций нормальные формы).является (2, 1)-вычислимым, но не (1, 1)-вычислимым. Аналогичные результаты получены для предикатов, описывающих вхождение ребра в минимальный путь между заданными вершинами графа.