|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
АЛГОРИТМ,Значение АЛГОРИТМ, в математической энциклопедии: алгорифм, Ч точное предписание, к-рое задает вычислительный процесс (называемый в этом случае алгоритмическим), начинающийся с произвольного исходного данного (из нек-рой совокупности возможных для данного А. исходных данных) и направленный на получение полностью определяемого этим исходным данным результата. А. являются, напр., известные из начальной школы правила сложения, вычитания, умножения и деления столбиком; в этих А. возможными результатами служат натуральные числа, записанные в десятичной системе, а возможными исходными данными - упорядоченные пары таких чисел.
Вообще говоря, не предполагается, что результат будет обязательно получен: процесс применения А. к конкретному возможному исходному данному (т. е. алгоритмич. процесс, развертывающийся начиная с этого данного) может также оборваться безрезультатно (в этом случае говорят, что произошла безрезультатная остановка) или не закончиться вовсе. В случае, если процесс заканчивается (соответственно не заканчивается) получением результата, говорят, что А. применим (соответственно неприменим) к рассматриваемому возможному исходному данному. (Можно построить такой А. Понятие А. занимает одно из центральных мест в современной математике, прежде всего вычислительной. Так, проблема численного решения уравнений данного типа заключается в отыскании А., к-рый всякую пару, составленную из произвольного уравнения этого типа и произвольного положительного рационального числа Пример алгоритма. Пусть возможными исходными данными и возможными результатами служат всевозможные слова в алфавите Значение алгоритмов. А. встречаются в науке на каждом шагу: умение решать задачу "в общем виде" всегда означает, по существу, владение нек-рым А. Говоря, напр., об умении человека складывать числа, имеют в виду не то, что он для любых чисел рано или поздно сумеет найти их сумму, а то, что он владеет нек-рым единообразным приемом сложения, применимым к любым двум конкретным записям чисел, т. е., иными словами, А. сложения (примером такого А. и является известное правило сложения чисел столбиком). Понятие задачи "в общем виде" уточняется при помощи понятия массовая алгоритмическая проблема (м. а. п.). М. а. п. задается серией отдельных, единичных проблем и состоит в требовании найти единый А. их решения (когда такого А. не существует, говорят, что рассматриваемая м. а. п. неразрешима). Так, проблема численного решения уравнений данного типа и проблема автоматического перевода суть м. а. п.: образующими их единичными проблемами являются в 1-м случае проблемы численного решения отдельных уравнений данного типа, а во 2-м случае - проблемы перевода отдельных фраз. Ролью м. а. <п. и определяется как значение, так и сфера приложения понятия А.: напр., а алгебре возникают м. а. п. проверки алгебраич. равенств различных типов, в математич. логике - м. а. п. распознавания выводимости предложений из заданных аксиом и т. п. (для математич. логики понятие А. существенно еще и потому, что на него опирается центральное для математич. логики понятие исчисления, служащее обобщением и уточнением интуитивных понятий "вывода", и "доказательства"). Установление неразрешимости к.-л. м. а. п. (напр., проблемы распознавания истинности или доказуемости для к.-л. логнко-математич. языка) является важным познавательным актом, показывающим, что для решения конкретных единичных проблем данной серии принципиально необходимы специфические для каждой отдельной проблемы методы. Содержательные явления, к-рые легли в основу образования понятия "А.", издавна занимали важное место в науке. С древнейших времен многие задачи математики заключались в поисках тех или иных конструктивных методов. Эти поиски, особенно усилившиеся в связи с созданием удобной символики, а также осмысления принципиального отсутствия искомых методов в ряде случаев (задача о квадратуре круга и подобные ей) - все это было мощным фактором развития научных знаний. Осознание невозможности решить задачу прямым вычислением привело к созданию в 19 в. теоретико-множественной концепции. Лишь после периода бурного развития этой концепции (в рамках к-рой вопрос о конструктивных методах в современном их понимании вообще не возникает) оказалось возможным в сер. 20 в. вновь вернуться к вопросам конструктивности, но уже на новом уровне, обогащенном выкристаллизовавшимся понятием А. Это понятие легло в основу конструктивного направления в математике. Само слово "А." происходит от algoritmi, являющегося, в свою очередь, латинской транслитерацией арабского имени хорезмийского математика 9 в. аль-Хорезми. В средневековой Европе А. назывались десятичная позиционная система счисления и искусство счета в ней, поскольку именно благодаря латинскому переводу (12 в.) трактата аль-Хорезми Европа познакомилась с позиционной системой. Строение алгоритмического процесса. Алгоритмич. процесс есть процесс последовательного преобразования конструктивных объектов (к. о.), происходящий дискретными "шагами"; каждый шаг состоит в смене одного к. о. другим. Так, при применении А. При этом в ряду сменяющих друг друга к. о. каждый последующий полностью определяется (в рамках данного А.) непосредственно предшествующим. При более строгом подходе предполагается также, что переход от каждого к. о. к непосредственно следующему достаточно "элементарен" - в том смысле, что происходящее за один шаг преобразование предыдущего к. о: в следующий носит локальный характер (преобразованию подвергается не весь к. о., а лишь нек-рая, заранее ограниченная для данного А. его часть, и само это преобразование определяется не всем предыдущим к. о., а лишь этой ограниченной частью). Таким образом, наряду с совокупностями возможных исходных данных и возможных результатов для каждого А. имеется еще совокупность возможных промежуточных результатов, представляющая собой ту рабочую среду, в к-рой развивается алгорит-мич. процесс. Для А. все три совокупности совпадают, а для А. вычитания столбиком - нет: возможными исходными данными служат пары чисел, возможными результатами - числа (все в десятичной системе), а возможные промежуточные результаты суть "трехэтажные" записи вида "Уточнения" понятия алгоритма. Понятие А. в его общем виде принадлежит к числу основных первоначальных понятий математики, не допускающих определения в терминах более простых понятий. Возможные уточнения понятия А. приводят, строго говоря, к известному сужению этого понятия. Каждое такое уточнение состоит в -том, что для каждого из указанных 7 параметров А. точно описывается нек-рый класс, в пределах к-рого этот параметр может меняться. Выбор таких классов и отличает одно уточнение от другого. Поскольку 7 параметров однозначно определяют нек-рый А., то выбор 7 классов изменения этих параметров определяет нек-рый класс А. Однако такой выбор может претендовать на название "уточнения", лишь если имеется убеждение, что для произвольного А., имеющего допускаемые данным выбором совокупности возможных исходных данных и возможных результатов, может быть указан равносильный ему А. из определенного данным выбором класса А. Это убеждение формулируется для каждого уточнения в виде основной гипотезы, к-рая - при современном уровне наших представлений - не может быть предметом математич-доказательства. Первые уточнения описанного типа предложили в 1936 Э. Л. Пост (Е. L. Post, см. [5]) и А. М. Тьюринг (А. М. Turing, см. [3], [4]), их конструкции во многом предвосхитили идеи, заложенные в основу современных цифровых вычислительных машин. Известны также уточнения, сформулированные А. А. Марковым (см. [10], [11], Нормальный алгорифм).и А. Н. Колмогоровым (см. [ 12], [ 13]; последний предложил трактовать конструктивные объекты как топологич. комплексы определенного вида, что дало возможность уточнить свойство "локальности" преобразования). Для каждого из предложенных уточнений соответствующая основная гипотеза хорошо согласуется с практикой. В пользу этой гипотезы говорит и то, что, как можно доказать, все предложенные уточнения в нек-ром естественном смысле эквивалентны друг другу. В качестве примера рассмотрим уточнение, предложенное А. М. Тьюрингом. В своем оригинальном виде это уточнение заключалось в описании нек-рой абстрактной вычислительной машины, состоящей из: 1) бесконечной ленты, разбитой на следующие друг за другом в линейном порядке ячейки, причем в каждой ячейке записан к.-л. символ из так наз. "внешнего алфавита" машины, и 2) каретки, находящейся в каждый момент в нек-ром "состоянии" (из заданного конечного списка состояний), способной перемещаться вдоль ленты и изменять содержимое ячеек; А. вычислений на такой машине ("тыорингов А.") задается в виде программы, управляющей действиями каретки. Более подробное и точное описание см. в статье Тьюринга машина;здесь приводится модернизированное изложение конструкции Тьюринга в терминах, указанных выше 7 параметров. Чтобы задать тыорингов А., надо указать: а) попарно непересекающиеся алфавиты Б, Д, Ч с выделенной в Дбуквой Лит. см. [3]-[5], [10]-[13] при СТ. Алгоритмов теория, В. А. Успенский. |
|
|
|

 , для к-рого не существует А., распознающего по произвольному возможному для
, для к-рого не существует А., распознающего по произвольному возможному для  исходному данному, применим к нему
исходному данному, применим к нему  или нет; такой А.
или нет; такой А.  можно, в частности, построить так, чтобы совокупностью его возможных исходных данных служил натуральный ряд.)
можно, в частности, построить так, чтобы совокупностью его возможных исходных данных служил натуральный ряд.) , перерабатывает в число (или набор чисел), отличающееся (отличающихся) от корня (корней) этого уравнения меньше, чем на
, перерабатывает в число (или набор чисел), отличающееся (отличающихся) от корня (корней) этого уравнения меньше, чем на  . Усовершенствование цифровых вычислительных машин дает возможность реализовать на них все более сложные А. Однако встретившийся в описывающей понятие А. формулировке термин "вычислительный процесс" не следует понимать в узком смысле только цифровых вычислений: уже в школьном курсе алгебры говорят о буквенных вычислениях, да и в арифметич. вычислениях появляются отличные от цифр символы (скобки, знак равенства, знаки арифметич. действий). Целесообразно, таким образом, рассматривать А., оперирующие с произвольными символами и их комбинациями. Простейшим случаем такой комбинации является линейная последовательность символов, образующая слово, однако можно рассматривать и "нелинейные" комбинации - такие, как алгебраич. матрицы, знакосочетания в смысле Н. Бурбаки (N. Bour-baki), фразы того или иного языка с расставленными стрелками синтаксич. управления и, вообще, размеченные тем или иным способом графы. Наиболее общее интуитивное понимание состоит в том, что исходными данными и результатами А. могут служить самые разнообразные конструктивные объекты. Это открывает возможность широкого применения понятия А. Можно говорить об А. перевода с одного языка на другой, об А. работы поездного диспетчера (перерабатывающего информацию о движении поездов в приказы) и др. примерах алгоритмич. описания процессов управления; именно поэтому понятие А. является одним из центральных понятий кибернетики.
. Усовершенствование цифровых вычислительных машин дает возможность реализовать на них все более сложные А. Однако встретившийся в описывающей понятие А. формулировке термин "вычислительный процесс" не следует понимать в узком смысле только цифровых вычислений: уже в школьном курсе алгебры говорят о буквенных вычислениях, да и в арифметич. вычислениях появляются отличные от цифр символы (скобки, знак равенства, знаки арифметич. действий). Целесообразно, таким образом, рассматривать А., оперирующие с произвольными символами и их комбинациями. Простейшим случаем такой комбинации является линейная последовательность символов, образующая слово, однако можно рассматривать и "нелинейные" комбинации - такие, как алгебраич. матрицы, знакосочетания в смысле Н. Бурбаки (N. Bour-baki), фразы того или иного языка с расставленными стрелками синтаксич. управления и, вообще, размеченные тем или иным способом графы. Наиболее общее интуитивное понимание состоит в том, что исходными данными и результатами А. могут служить самые разнообразные конструктивные объекты. Это открывает возможность широкого применения понятия А. Можно говорить об А. перевода с одного языка на другой, об А. работы поездного диспетчера (перерабатывающего информацию о движении поездов в приказы) и др. примерах алгоритмич. описания процессов управления; именно поэтому понятие А. является одним из центральных понятий кибернетики. . Условимся называть переход от слова Xк слову Y"допустимым" в следующих двух случаях (ниже Робозначает произвольное слово): 1) X имеет вид аР, а Y имеет вид Рb;2) Xимеет вид bаР, a Y имеет вид Раbа. Формулируется предписание: "взяв к.-л. слово в качестве исходного, делай допустимые переходы до тех пор, пока не получится слово вида ааР;тогда остановись, слово Ри есть результат". Это предписание образует А., к-рый обозначим
. Условимся называть переход от слова Xк слову Y"допустимым" в следующих двух случаях (ниже Робозначает произвольное слово): 1) X имеет вид аР, а Y имеет вид Рb;2) Xимеет вид bаР, a Y имеет вид Раbа. Формулируется предписание: "взяв к.-л. слово в качестве исходного, делай допустимые переходы до тех пор, пока не получится слово вида ааР;тогда остановись, слово Ри есть результат". Это предписание образует А., к-рый обозначим  . Возьмем в качестве исходного данного слово bаbаа. После одного перехода получим bаааbа, после второго ааbааbа. В силу предписания мы должны остановиться, результат есть bааbа. Возьмем в качестве исходного данного слово bааbа. Получим последовательно аbааbа, bааbаb, аbаbаbа, bаbаbаb, bаbаbаbа,.... Можно доказать, что процесс никогда не кончится (т. е. никогда не возникает слово, начинающееся с аа, и для каждого из получающихся слов можно будет совершить допустимый переход). Возьмем теперь в качестве исходного данного слово аbааb. Получим bааbb, аbbаbа, bbаbаb. Далее мы не можем совершить допустимый переход, и в то же время нет сигнала остановки. Произошла безрезультатная остановка. Итак,
. Возьмем в качестве исходного данного слово bаbаа. После одного перехода получим bаааbа, после второго ааbааbа. В силу предписания мы должны остановиться, результат есть bааbа. Возьмем в качестве исходного данного слово bааbа. Получим последовательно аbааbа, bааbаb, аbаbаbа, bаbаbаb, bаbаbаbа,.... Можно доказать, что процесс никогда не кончится (т. е. никогда не возникает слово, начинающееся с аа, и для каждого из получающихся слов можно будет совершить допустимый переход). Возьмем теперь в качестве исходного данного слово аbааb. Получим bааbb, аbbаbа, bbаbаb. Далее мы не можем совершить допустимый переход, и в то же время нет сигнала остановки. Произошла безрезультатная остановка. Итак,  применим к слову bаbаа и неприменим к словам bааbа и аbааb.
применим к слову bаbаа и неприменим к словам bааbа и аbааb. к слову baaba возникают последовательно baaba, abaaba, bааbаb и т. д. А при применении, скажем, А. вычитания столбиком к паре (307, 49) последовательно возникнут такие к. о.:
к слову baaba возникают последовательно baaba, abaaba, bааbаb и т. д. А при применении, скажем, А. вычитания столбиком к паре (307, 49) последовательно возникнут такие к. о.:
 где
где  - запись числа в десятичной системе,
- запись числа в десятичной системе, 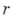 - такая же запись или пустое слово, а р - запись числа в десятичной системе с допущением точек над нек-рыми цифрами. Как правило, для данного А. можно выделить 7 характеризующих его (не независимых) параметров: 1) совокупность возможных исходных данных, 2) совокупность возможных результатов, 3) совокупность возможных промежуточных результатов, 4) правило начала, 5) правило непосредственной переработки, 6) правило окончания, 7) правило извлечения результата.
- такая же запись или пустое слово, а р - запись числа в десятичной системе с допущением точек над нек-рыми цифрами. Как правило, для данного А. можно выделить 7 характеризующих его (не независимых) параметров: 1) совокупность возможных исходных данных, 2) совокупность возможных результатов, 3) совокупность возможных промежуточных результатов, 4) правило начала, 5) правило непосредственной переработки, 6) правило окончания, 7) правило извлечения результата.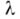 и выделенными в Чбуквами
и выделенными в Чбуквами  и
и  , б) набор пар вида
, б) набор пар вида  , где
, где 
 , а Тесть один из трех знаков - , 0, +, причем предполагается, что в этом наборе (наз. программой) нет 2 пар с одинаковыми первыми членами. Параметры А. задаются так: возможными исходными данными и возможными результатами служат слова в Б, а возможными промежуточными результатами - слова в алфавите
, а Тесть один из трех знаков - , 0, +, причем предполагается, что в этом наборе (наз. программой) нет 2 пар с одинаковыми первыми членами. Параметры А. задаются так: возможными исходными данными и возможными результатами служат слова в Б, а возможными промежуточными результатами - слова в алфавите  содержащие не более одной буквы из Ч. Правило начала: исходное слово Рпереводится в слово
содержащие не более одной буквы из Ч. Правило начала: исходное слово Рпереводится в слово  . Правило окончания: заключительным является промежуточный результат, содержащий со. Правило извлечения результата: результатом объявляется цепочка всех тех букв заключительного промежуточного результата, к-рая идет вслед за w и предшествует первой букве, не принадлежащей Б. Правило непосредственной переработки, переводящее
. Правило окончания: заключительным является промежуточный результат, содержащий со. Правило извлечения результата: результатом объявляется цепочка всех тех букв заключительного промежуточного результата, к-рая идет вслед за w и предшествует первой букве, не принадлежащей Б. Правило непосредственной переработки, переводящее  , состоит в следующем. Приписываем к Аслева и справа букву
, состоит в следующем. Приписываем к Аслева и справа букву  ; затем в образовавшемся слове часть вида
; затем в образовавшемся слове часть вида  , где
, где  ,
,  , заменяем на слово Qпо следующему правилу: в программе ищется пара с первым членом
, заменяем на слово Qпо следующему правилу: в программе ищется пара с первым членом  ; пусть второй член этой пары есть
; пусть второй член этой пары есть  ; если
; если  есть -, то
есть -, то  ; если Тесть 0, то
; если Тесть 0, то  ; если Тесть +, то
; если Тесть +, то 
 Возникающее после этой замены слово и есть А'.
Возникающее после этой замены слово и есть А'.