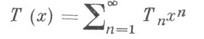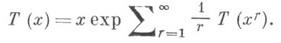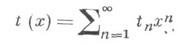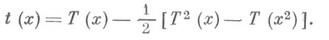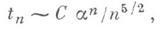ДЕРЕВО

Значение ДЕРЕВО в математической энциклопедии:

в теории графов - связный неориентированный граф G, не содержащий циклов. Д. не имеет кратных ребер и петель. Являясь простейшими связными графами, Д. служат хорошими моделями для рассмотрения различных вопросов теории графов. Любое Д. с пвершинами содержит п-1 ребер. Число различных Д., к-рые можно построить на пнумерованных вершинах, равно n^n-2. Д. с одной выделенной вершиной наз. корневым деревом.

Перечисляющий ряд

для числа Т _n неизоморфных корневых Д. с пвершинами удовлетворяет функциональному уравнению

Перечисляющий ряд

для числа t_n неизоморфных Д. с n вершинами можно представить с помощью перечисляющего ряда для корневых Д.:

Функциональные уравнения для Т(х)и t(x)позволяют вычислять значения Т _п и t_n для конкретных значений п(см., напр., [1]). Доказано, что при

где С=0,534948;.., a=2,95576... (см. [2]). Задачи перечисления Д. определенного вида возникают, напр., в химии при изучении изомеров.

Д. можно достаточно просто кодировать наборами из нулей и единиц. Рассмотрим, напр., к.-л. правильную (без пересечения ребер) укладку Д. Dна плоскости (см. Графа укладка). Начиная с к.-л. вершины, будем двигаться по ребрам Д. D, сворачивая в каждой вершине на ближайшее справа ребро и поворачивая назад в концевых вершинах Д. Проходя по нек-рому ребру, записываем 0 при движении по ребру в первый раз и 1 при движении по ребру второй раз (в обратном направлении). Если m- число ребер Д. D, то через 2т шагов мы вернемся в исходную вершину, пройдя по каждому ребру дважды. Полученная при этом последовательность из 0 и 1 (код Д.) длины 2m позволяет однозначно восстанавливать не только само Д. D, но и его укладку на плоскости. Произвольному Д. соответствуют несколько кодов. Из этого способа кодирования вытекает оценка: t_n<T_n<4ⁿ.

Д. Gс пвершинами однозначно восстанавливается (с точностью до изоморфизма) по набору всех его (п-1)-вершинных подграфов G-v, получаемых из Gудалением каждой из его вершин v.

Любое Д. однозначно определяется также расстояниями (длиной наименьшей цепи) между его концевыми (степени 1) вершинами.

Остовное дерево (остов) - это подграф данного графа, содержащий все его вершины и являющийся Д. Число остовных Д. произвольного связного графа Gбез петель и кратных ребер можно вычислить следующим образом. Пусть М- матрица, полученная из матрицы смежности графа Gизменением знаков всех элементов на противоположный и заменой i-го элемента главной диагонали степенью вершины v_i. Тогда алгебраич. дополнения всех элементов главной диагонали матрицы Мравны между собой и их общее значение есть число остовов графа G. Остовные Д. используются, напр., для нахождения независимых циклов в электрич. схеме.

Важное значение для приложений имеет задача нахождения в связном графе, ребрам к-рого приписаны веса, остовного Д. с наименьшей суммой весов ребер. Такая задача возникает, напр., при проектировании коммуникационных сетей. Известен алгоритм для решения этой задачи о кратчайшем связывающем дереве (см. [3]). Д., растущим (или выходящим) из вершины u₀, наз. ориентированный граф, к-рый является (без учета ориентации) корневым Д. с корнем u₀ и в к-ром для любой вершины u₁ (единственная) цепь, соединяющая v₀ с v₁, является ориентированным путем из v₀ в v₁. Такие Д. используются, напр., для описания детерминированных функций, для представления информации в информационно-поисковых системах и т. д.

Обобщением понятия "Д." является понятие "леса"; лес - это граф без циклов (не обязательно связный).

Лит.:[1] ХарариФ., Теория графов, пер. с англ., М., 1973 (лит.); [2] Otter R., "Ann. Math.", 1948, v. 49, № 3, p. 583-99; [3] Прим Р. К., "Кибернетический сборник", 1961. в. 2, с. 95 - 107.

В. Б. Алексеев.