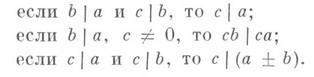|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ДЕЛИМОСТЬЗначение ДЕЛИМОСТЬ в математической энциклопедии: в кольце - обобщение понятия делимости целых чисел нацело (см. Деление). Элемент акольца Аделится на другой элемент В любом ассоциативно-коммутативном кольце имеют место следующие свойства Д.:
Последние два свойства равносильны тому, что множество элементов, делящихся на b, образует идеал bА кольца А(главный идеал, порожденный элементом b), к-рый содержит b, если А- кольцо с единицей. В области целостности элементы аи bделятся друг на друга одновременно ( а|b и b|а )тогда и только тогда, когда они ассоциированы, т. е. a=eb, где e - обратимый элемент. Два ассоциированных элемента порождают один и тот же главный идеал. Делители единицы совпадают, по определению, с обратимыми элементами. Простым элементом в кольце наз. ненулевой элемент, не имеющий собственных делителей, кроме делителей единицы. В кольце целых чисел такие элементы наз. простыми числами, в кольце многочленов - неприводимыми многочленами. Кольца, в к-рых подобно кольцу целых, чисел или кольцу многочленов имеет место однозначное разложение на простые множители (с точностью до делителей единицы и порядка следования), наз. факториалъными кольцами. В таком кольце для всякой конечной совокупности элементов существуют наибольший общий делитель и наименьшее общее кратное, оба определенные однозначно с точностью до делителей единицы. Лит.:[1] Kummer E., "J. reine und angew. Math.", 1847, Bd 35, S. 319-26; [2] Виноградов И. М., Основы теории чисел, 8 изд., М., 1972; [3] Боревич 3. И., Шафаревич И. Р., Теория чисел, 2 изд., М., 1972. О. А. Иванова, С. А. Степанов. |
|
|
|

 если существует такой
если существует такой 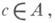 что а=bс. При этом говорят также, что 6 делит а, и аназ. кратным элемента b, а b - делителем элемента а. Для обозначения Д. ана bупотребляют символ b|а.
что а=bс. При этом говорят также, что 6 делит а, и аназ. кратным элемента b, а b - делителем элемента а. Для обозначения Д. ана bупотребляют символ b|а.