ДЕЛИМОСТИ ПРИЗНАК

Значение ДЕЛИМОСТИ ПРИЗНАК в математической энциклопедии:

на натуральное число d- условие, к-рому удовлетворяет натуральное число Ав том и только в том случае, если оно делится на d. Желательно, чтобы это условие можно было легко проверить и чтобы эта проверка была не сложнее непосредственного деления числа Ана d

Если разность чисел Аи Вделится на d, то число Аделится на dтогда и только тогда, когда число Вделится на d. На этом свойстве основан вывод многих Д. п. Пусть запись числа Ав десятичной системе счисления имеет вид:

тогда

Из этих равенств сразу получаются Д. п. на делители чисел 10, 100, 1000,... В частности, для. того чтобы число А делилось на2, необходимо и достаточно, чтобы его последняя цифра, т. е. число а ₀, делилось на 2; для того чтобы число A делилось на 4 {н а 8), необходимо и достаточно, чтобы число, изображаемое двумя (соответственно тремя) последними цифрами числа А, т. е. число а ₀+10а ₁, делилось на 4 {соответственно а ₀+10а ₁+100а ₂ делилось на 8). Так как разность (а ₀+10а ₁ )-(а ₀+2а ₁). кратна 4, то Д. п. на 4 можно дать и в такой форме: число Аделится на 4 тогда и только тогда, когда число а ₀+2а ₁ делится на 4. Каждый Д. п. на число dпозволяет сопоставить с числом А, если оно не слишком мало, нек-рое неотрицательное целое число, меньшее А, к-рое делится на dв том и только в том случае, когда само число Аделится на d. Другими словами, каждый Д. п. на число dопределяется нек-рой функцией f, принимающей целые значения и удовлетворяющей условиям: |f(A)|<A для каждого натурального А, начиная с некоторого; f(A) делится на dтогда и только тогда, когда число Аделится на d. Любая целозначная функция, удовлетворяющая перечисленным условиям, наз. функцией делимости на число d;. множество всех таких функций обозначается W(d). Ясно, что

Поскольку

то

Итак, число Аделится на 3 (на 9) тогда и только тогда, когда сумма цифр этого числа делится на 3 (соответственно на 9). Аналогично,

Следовательно,

Используя представления чисел в системе счисления с основанием 10^k, где k=2,3,. . ., можно найти Д. п. на делители чисел вида 10^k+1. Так, при к = 2 получаются следующие функции делимости на 11 и 101:

Поскольку 10³ +1 = 7-11 -13, получается объединенный Д. п. на числа 7, 11, 13: чтобы узнать, делится ли данное число на какое-нибудь из чисел 7, 11 или 13, достаточно разбить цифры этого числа на грани, начиная справа, по три в каждой, а Затем соединить попеременно знаками+и - числа, образованные этими гранями. Полученное число делится на 7, 11 или 13 тогда и только тогда, когда данное число делится соответственно на 7, 11 или 13. Таким образом,

Если целые числа си d взаимно просты, то число Ас делится на dтогда и только тогда, когда число Аделится на d. Это соображение также часто используется при построении Д. п. Пусть d- какой-нибудь делитель разности 10с - 1, тогда числа си d взаимно просты, и из равенства

следует, что число Аделится на dв том и только в том случае, если число А ₁+са ₀ делится на d. Напр., при d=19, с=2 разность 10с-1 делится на 19. Поэтому

Чтобы узнать, делится ли число на 19, можно последовательно применять этот признак. Пусть d- какой-нибудь делитель суммы 10c+l. Из равенства

следует, что число Аделится на dтогда и только тогда, когда число А ₁ - са ₀ делится на d. Так, при с= 11 число 10c+l делится на 37. Поэтому

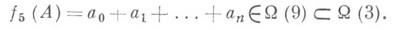
Соответствующий 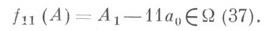Д. п. можно сформулировать так: чтобы узнать, делится ли число Ана 37 или нет, достаточно вычеркнуть последнюю цифру числа Аи из числа, образуемого невычеркнутыми цифрами, вычесть произведение 11 на число, изображаемое вычеркнутой цифрой. Число Аделится на 37 в том и только в том случае, если полученное число делится на 37. Подобным образом можно вывести Д. п. и на делители чисел вида

Лит.:[1] Воробьев Н. Н., Признаки делимости, 2 изд., М., 1974.

В. И. Нечаев.