|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ДВОЙНОЙ РЯДЗначение ДВОЙНОЙ РЯД в математической энциклопедии: - ряд
члены и тп, т, n=1, 2, ..., к-рого образуют двойную числовую последовательность. Конечные суммы
наз. частичными суммами Д. р. (1), или прямоугольными частичными суммами. Они также образуют двойную последовательность. Если у этой последовательности {Smn} существует конечный двойной предел
то ряд (1) наз. сходящимся, а число S- его суммой:
Если конечного предела (2) не существует, то ряд (1) наз. расходящимся. На Д. р. переносятся многие свойства обычных (однократных) рядов. Напр., если Д. р. сходятся, то при любых числах lи mД. р.
также сходится и
Если Д. р. сходится, то
(необходимое условие сходимости ряда (1)). Для того чтобы Д. р. (1) сходился, необходимо и достаточно, чтобы для любого е>0 существовало такое число Ne, что
Д. р. обладают свойствами, обусловленными наличием у его членов двух индексов, к-рые являются специфич. особенностью Д. р. Если сходится Д. р. (1) и для всех n=1, 2, ... сходятся ряды
то повторный ряд
также сходится и его сумма равна сумме данного ряда. Д. р. наз. абсолютно сходящимся, если сходится ряд Если Д. р. абсолютно сходится, то он и просто сходится; более того, сходится любой ряд, полученный перестановкой членов данного Д. р. При этом сумма любого такого ряда совпадает с суммой исходного ряда. На Д. р., члены к-рых являются функциями, переносятся многие понятия и свойства, присущие обычным функциональным рядам, напр., понятие равномерной сходимости, критерий Коши равномерной сходимости ряда, признак Вейерштрасса равномерной сходимости. Вместе с тем, далеко не все теоремы об однократных рядах непосредственно переносятся на Д. р. Так, прямой аналог Абеля теоремы для степенных рядов не справедлив для двойных степенных рядов, т. е. рядов вида
Существуют, напр., Д. р. (3), к-рые сходятся только в двух точках плоскости: ряд (3) с коэффициентами
сходится только в двух точках (0, 0) и (1, 1). Кроме определения (2) для Д. р. (1) существуют другие определения его сходимости и суммы, связанные также с наличием у его членов двух индексов. Напр., пусть
(Sp наз. треугольной частичной суммой Д. р. (1)), то Д. р. (1) наз. сходящимся, если последовательность {S р} сходится; ее предел
наз. треугольной суммой ряда (1). Если положить
(Sr наз. круговой частичной суммой), то Д. р. (1) наз. сходящимся, если функция Sr параметра rимеет предел при
наз. круговой суммой ряда (1). Если через
то число Sназ. суммой ряда (1), если для любого e>0 существует такое копечное множество Все эти определения сходимости Д. р. (1) не эквивалентны между собой. Однако, если члены Д. р. неотрицательны, то из сходимости в одном из указанных смыслов следует сходимость во всех остальных, причем все значения сумм Д. р. (1) в этом случае совпадают. Имеются и другие определения сходимости Д. р. Для Д. р. существуют различные методы суммирования. Понятие Д. р. обобщается на случай, когда его члены являются не числами, а, напр., элементами линейного нормированного пространства. Лит.:[1] Pringsheim A., "Munchener Sitzungsber. der Math.", 1897, Bd 27, S. 101-53; [2] его же, "Math. Ann.", 1900, Bd 53, S. 289-321; [3] его же, Vorlesungen uber Zahlenlehre, Bd 2, Lpz.- В., 1923; [4] Вrоmwiсh Т. J., Theory of infinite series, 2 ed., L., 1926; [5] Салехов Г. С, Вычисление рядов, М., 1955; [6] Уиттекер Э.-Т., Ватсон Д.-Н., Курс современного анализа, пер. с англ., 2 изд., т. 1, М., 1903. Л. Д. Кудрявцев. |
|
|
|









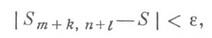 если только m>Ne, n>Ne, а kи l- любые неотрицательные целые. Если все члены ряда (1) неотрицательны, то последовательность его частичных сумм Smn всегда имеет конечный или бесконечный предел, причем
если только m>Ne, n>Ne, а kи l- любые неотрицательные целые. Если все члены ряда (1) неотрицательны, то последовательность его частичных сумм Smn всегда имеет конечный или бесконечный предел, причем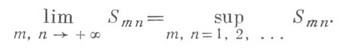


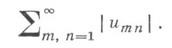






 этот предел
этот предел
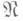 обозначить произвольное конечное множество пар индексов ( т, п )и положить
обозначить произвольное конечное множество пар индексов ( т, п )и положить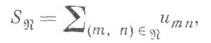
 пар индексов (то, п), что для любого
пар индексов (то, п), что для любого  выполняется неравенство
выполняется неравенство  Если такое число Sсуществует, то ряд (1) наз. сходящимся.
Если такое число Sсуществует, то ряд (1) наз. сходящимся.