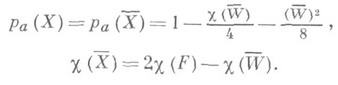ДВОЙНАЯ ПЛОСКОСТЬ

Значение ДВОЙНАЯ ПЛОСКОСТЬ в математической энциклопедии:

- алгебраическая поверхность, представляющая собой двумерный аналог гиперэллиптической кривой. Неособая алгебраическая проективная поверхность Xнад алгебраически замкнутым полем кназ. двойной плоскостью, если ее поле рациональных функций k(X)является квадратичным расширением поля рациональных функций от двух переменных. Если характеристика поля отлична от 2 (в дальнейшем это условие предполагается выполненным), то каждая Д. п. бирационально изоморфна аффинной поверхности, задаваемой в трехмерном аффинном пространстве уравнением

Иногда именно поверхности такого типа наз. Д. п. Для каждой Д. п. Xсуществует морфизм f в проективную плоскость Р ²(k), разлагающийся в композицию бирациоьального морфизма

на некоторую нормальную поверхность X' и конечного морфизма степени два

Кривая ветвления Wморфизма j' наз. кривой ветвления Д. п. (и определяется, вообще говоря, не однозначно по X). Кривая ветвления Д. п. играет основную роль в их изучении. Напр., по ней вычисляются численные инварианты Д. п. Если Wнеприводима, то иррегулярность Д. п. Xравна нулю. Если степень W(всегда четная) равна 2k и все особенности Wтолько двойные обыкновенные или каспидальные (см. Особая точка алгебраической кривой), то арифметич. род р _а (Х). и эйлерова характеристика c(X)(топологическая или l-адическая) вычисляются по формулам:

В общем случае существует бирационалышй морфизм такой, что проекция на Fнормализации Xрасслоенного произведения Xи Fнад Р ²(k)на Fявляется конечным накрытием степени 2 с неособой (быть может, приводимой) кривой ветвления W. В этом случае имеют место формулы:

Для любой кривой Wчетной степени на проективной плоскости всегда существует Д. п., имеющая Wв качестве своей кривой ветвления. Выбор подходящей кривой Wпозволяет во многих случаях решать задачу построения алгебраич. поверхности с заданными инвариантами (см. [1], [3]).

Классификация Д. п. проводится отдельно в каждом классе алгебраич. поверхностей. Описаны [5] рациональные и линейчатые Д. п.; перечислены [3] Д. п., являющиеся эллиптическими поверхностями или КЗ-поверхностями. Рассмотрено (см. [3], [4]) много примеров Д. п. основного типа.

Лит.:[1] Итоги науки. Алгебра. Топология. Геометрия, т. 12, М., 1974, с. 77-170; [2] ZariskiO., Algebraic surfaces, В., 1971; [3] Enriaues F., Le superficie algebriche, Bologna, 1949; [4] Campedelli L., "Atti Accad. naz. Lincei Rend.", ser. 6, 1932, v. 15, p. 203-8, 358-62, 536-42; [5] Jung H. W. E., "J. reine und angew. Math.", 1942, Bd 184, №4, S. 199 - 237.

И. В. Долгачев.