|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ДАНИЕЛЯ ИНТЕГРАЛЗначение ДАНИЕЛЯ ИНТЕГРАЛ в математической энциклопедии: - расширение понятия интеграла, предложенное П. Даниелем [1]. Схема построения этого интеграла наз. схемой Даниеля, представляет собой продолжение на более широкий класс функций интеграла, определенного первоначально для нек-рой совокупности функций, называемых элементарными функциями. При сохранении способа продолжения изменение объема исходной совокупности элементарных функций приводит к разным расширениям понятия интеграла. В этой схеме аксиоматизируется понятие элементарного интеграла, в отличие от схемы Лебега (см. Лебега интеграл), аксиоматизирующей понятие меры. Пусть X- произвольное множество и L0- некоторая совокупность определенных на Xдействительных ограниченных функций; эти функции наз. элементарными. Предполагается, что L0- векторная решетка, т. <е. из f,
Пусть на L0 определен функционал I(f), принимающий действительные значения и такой, что
если Такой функционал наз. интегралом от элементарных функций, или элементарным интегралом. Множество
Функция f(x), определенная на X, принадлежит классу L+, если существует такая последовательность
наз. интегралом от f. Интеграл I(f) не зависит от выбора аппроксимирующей последовательности {fn}. Классом Lназ. совокупность функций f, определенных на Xи представимых в виде f=f1-f2, где
Класс Lс точностью до множества меры нуль является векторной решеткой конечных функций, замкнутой относительно сходимости почти всюду с ограниченными интегралами, и Д. и. от суммируемых функций обладает свойствами дистрибутивности, неотрицательности, непрерывности (относительно сходимости почти всюду), мажорированной суммируемой функцией (теорема Лебега о переходе к пределу под знаком интеграла), а также рядом других естественных свойств интеграла. В том случае, когда Х=[ а, b]и L0 есть совокупность ступенчатых функций
Д. и. совпадает с интегралом Лебега от функций, суммируемых на [ а, b]. Схема Даниеля применима для построения интеграла от функций со значениями в s-полной решетке. Лит.:[1] Daniеll P., "Ann. Math.", 1917, v. 19, p. 279 -94; [2] Шилов Г. Е., Гуревич Б. Л., Интеграл, мера и производная, 2 изд., М., 1967; [3] Люмис Л., Введение в абстрактный гармонический анализ, пер. с англ., М., 1956. В. И. Соболев. |
|
|
|

 и
и 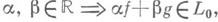
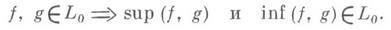

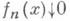 для любого х, то
для любого х, то 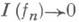 (непрерывность относительно монотонной сходимости).
(непрерывность относительно монотонной сходимости). наз. множеством меры нуль, если для любого e>0 найдется такая неубывающая последовательность
наз. множеством меры нуль, если для любого e>0 найдется такая неубывающая последовательность  что sup
что sup 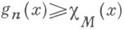 , где cM (х)- характеристич. функция множества М:
, где cM (х)- характеристич. функция множества М:
 что
что  почти всюду и
почти всюду и  . Число
. Число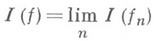
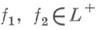 . Функции класса Lназ. суммируемыми, а число
. Функции класса Lназ. суммируемыми, а число - интегралом Даниеля от функции f.
- интегралом Даниеля от функции f.