|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ДАНЖУА - ЛУЗИНА ТЕОРЕМАЗначение ДАНЖУА - ЛУЗИНА ТЕОРЕМА в математической энциклопедии: об абсолютно сходящихся тригонометрич. рядах: если тригонометрич. ряд
сходится на множестве положительной меры Лебега, то ряд, составленный из абсолютных величин его коэффициентов
сходится и, следовательно, исходный ряд (1) сходится абсолютно и равномерно на всей числовой оси. Свойство положительности меры множества сходимости ряда (1), будучи, согласно Д.- Л. т., достаточным для сходимости ряда (2), не является, однако, необходимым. Существуют, напр., совершенные множества меры нуль, из сходимости на к-рых ряда (1) следует сходимость ряда (2). Теорема установлена независимо А. Данжуа [1] и Н. Н. Лузиным [2]; имеются различные ее обобщения (см. [3]). Лит.:[1] D enjоу А., "С. г. Acad. sci.", 1912, t. 155, p. 135 - 6; [2] Лузин Н. Н., "Матем. сб.", 1912, т. 28, с. 461-72; [3] Бари Н. К., Тригонометрические ряды, М., 1961. Л. Д. Кудрявцев, Е. М. Никишин. |
|
|
|

 (1)
(1)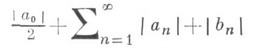 (2)
(2)