|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
Д'АЛАМБЕРА ПРИНЦИПЗначение Д'АЛАМБЕРА ПРИНЦИП в математической энциклопедии: - один из основных принципов динамики несвободных механич. систем; он содержит общий метод, с помощью к-рого уравнения движения любой механич. системы можно вывести в виде уравнений равновесия сил (и в этом смысле Д. п. сводит динамику к статике), а также определить реакции связей. Принцип сформулирован Ж. Д'Аламбером [1] в виде правила для определения движений (под к-рыми понимаются векторы скоростей) нескольких тел, действующих одно на другое при помощи нитей или жестких стержней: движения, передаваемые телам, раскладывают каждое на два движения - на движение, фактически воспринятое телами, и на нек-рое другое, причем эти два движения должны быть таковыми, что если телам будет передано лишь первое движение, то тела могут совершать это движение, не мешая одно другому, если же телам передано лишь второе движение, то тела будут оставаться в покое. Д. п. был успешно применен Ж. Д'Аламбером и другими учеными при решении ряда задач. Однако разложение движений, требуемое принципом, и определение тех сил, к-рые должны уничтожаться, представляют трудную задачу. Это побудило Ж. Лагранжа [2] предложить иную формулировку Д. п., основанную на установлении равновесия между силами и вызванными ими движениями, но направленными противоположно, к-рая близка к современной. Если обозначить через
т. е. в каждый момент времени заданная активная сила и реакция связей, приложенные к движущейся материальной точке, уравновешиваются силой инерции -
то равенства (*) примут вид:
т. е. в каждый момент времени "потерянная сила" Лит.:[1] D'Alembert J., Traite de dynamique, P., 1743 (рус. пер.: Даламбер Ж., Динамика, М.-Л., 1950); [2] Lagrange J., Mecanique analytique, P., 1788 (рус. пер.: Лагранж Ж., Аналитическая механика, т. 1, 2 изд., М.-Л., 1950); [3] Суслов Г. К., Теоретическая механика, 3 изд., М.-Л., 1946. В. В. Румянцев. |
|
|
|

 и
и 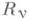 заданную активную силу и реакцию связей, действующие на движущуюся с ускорением
заданную активную силу и реакцию связей, действующие на движущуюся с ускорением  материальную точку с массой
материальную точку с массой  , то, согласно Д. п.,
, то, согласно Д. п.,
 точки. Или, если разложить силу на
точки. Или, если разложить силу на  две составляющие силы:
две составляющие силы:

 уравновешивается силой реакции связей (см. [3]).
уравновешивается силой реакции связей (см. [3]).