"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ГРУППОВОЙ ОБЪЕКТ
Значение ГРУППОВОЙ ОБЪЕКТ в математической энциклопедии:
категории - объект Xкатегории Стакой, что для любого  множество морфизмов
множество морфизмов  является группой, а соответствие
является группой, а соответствие  - функтором из категории Св категорию групп (Gr). Гомоморфизмом Г. о. X в Г. о. У наз. такой морфизм
- функтором из категории Св категорию групп (Gr). Гомоморфизмом Г. о. X в Г. о. У наз. такой морфизм  категории С, что для любого
категории С, что для любого  соответствующее отображение
соответствующее отображение  является гомоморфизмом групп. Г. <о. категории Собразуют подкатегорию
является гомоморфизмом групп. Г. <о. категории Собразуют подкатегорию 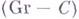 категории С; морфизмами в этой категории служат гомоморфизмы. Функтор
категории С; морфизмами в этой категории служат гомоморфизмы. Функтор  устанавливает эквивалентность категории
устанавливает эквивалентность категории  и категории представимых предпучков групп на категории С. В случае, когда значения функтора
и категории представимых предпучков групп на категории С. В случае, когда значения функтора  принадлежат подкатегории
принадлежат подкатегории  абелевых групп, Г. о. Xяаз. коммутативным, или абелевым. Если категория Собладает конечными произведениями и финальным объектом е, то Г. о. Xкатегории Сопределяются следующими свойствами.
абелевых групп, Г. о. Xяаз. коммутативным, или абелевым. Если категория Собладает конечными произведениями и финальным объектом е, то Г. о. Xкатегории Сопределяются следующими свойствами.
Существуют морфизмы  (умножение),
(умножение),  (обращение) и
(обращение) и  (единица), к-рые удовлетворяют следующим аксиомам.
(единица), к-рые удовлетворяют следующим аксиомам.
а) Ассоциативность. Диаграмма коммутативна.

б) Существование единичного элемента. Диаграмма коммутативна.

в) Существование обратного элемента. Диаграмма

коммутативна. Здесь всюду  - канонический морфизм объекта X в финальный объект
- канонический морфизм объекта X в финальный объект 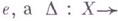
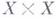 - диагональный морфизм.
- диагональный морфизм.
В случае, когда Сесть категория множеств (Ens), Г. о. Xсуть в точности группы. Финальным объектом категории (Ens) является множество  , состоящее из одного элемента е. Аксиома а) означает ассоциативность бинарной операции, задаваемой морфизмом
, состоящее из одного элемента е. Аксиома а) означает ассоциативность бинарной операции, задаваемой морфизмом 
 . Морфизм
. Морфизм  есть отображение обращения, а морфизм
есть отображение обращения, а морфизм  есть отображение множества
есть отображение множества  в X, образ к-рого равен единичному элементу в X.
в X, образ к-рого равен единичному элементу в X.
Аналогичным способом можно определить кольцевой объект категории и вообще задать алгебраическую структуру на объекте категории (см. [2]).
Лит.:[1] Манин Ю. И., "Успехи матем. наук", 1963, т. 18, в. 6; [2] Demazure M., Grot, hendieck A., Schemas en groupes, t. 1, В.- Hdlb.- N.Y., 1970. И. В. Долгачев.

 множество морфизмов
множество морфизмов  является группой, а соответствие
является группой, а соответствие  - функтором из категории Св категорию групп (Gr). Гомоморфизмом Г. о. X в Г. о. У наз. такой морфизм
- функтором из категории Св категорию групп (Gr). Гомоморфизмом Г. о. X в Г. о. У наз. такой морфизм  категории С, что для любого
категории С, что для любого  соответствующее отображение
соответствующее отображение  является гомоморфизмом групп. Г. <о. категории Собразуют подкатегорию
является гомоморфизмом групп. Г. <о. категории Собразуют подкатегорию 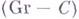 категории С; морфизмами в этой категории служат гомоморфизмы. Функтор
категории С; морфизмами в этой категории служат гомоморфизмы. Функтор  устанавливает эквивалентность категории
устанавливает эквивалентность категории  и категории представимых предпучков групп на категории С. В случае, когда значения функтора
и категории представимых предпучков групп на категории С. В случае, когда значения функтора  принадлежат подкатегории
принадлежат подкатегории  абелевых групп, Г. о. Xяаз. коммутативным, или абелевым. Если категория Собладает конечными произведениями и финальным объектом е, то Г. о. Xкатегории Сопределяются следующими свойствами.
абелевых групп, Г. о. Xяаз. коммутативным, или абелевым. Если категория Собладает конечными произведениями и финальным объектом е, то Г. о. Xкатегории Сопределяются следующими свойствами. (умножение),
(умножение),  (обращение) и
(обращение) и  (единица), к-рые удовлетворяют следующим аксиомам.
(единица), к-рые удовлетворяют следующим аксиомам.


 - канонический морфизм объекта X в финальный объект
- канонический морфизм объекта X в финальный объект 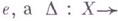
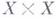 - диагональный морфизм.
- диагональный морфизм. , состоящее из одного элемента е. Аксиома а) означает ассоциативность бинарной операции, задаваемой морфизмом
, состоящее из одного элемента е. Аксиома а) означает ассоциативность бинарной операции, задаваемой морфизмом 
 . Морфизм
. Морфизм  есть отображение обращения, а морфизм
есть отображение обращения, а морфизм  есть отображение множества
есть отображение множества  в X, образ к-рого равен единичному элементу в X.
в X, образ к-рого равен единичному элементу в X.