|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ГРУППОВОЕ ИСЧИСЛЕНИЕЗначение ГРУППОВОЕ ИСЧИСЛЕНИЕ в математической энциклопедии: ассоциативное исчисление, в к-ром эффективным образом выполнено естественное групповое требование существования обратной операции. Именно, ассоциативное исчисление наз. Г. и. (см. [1], с. 341), если для него может быть построен инвертирующий алгоритм, т. е. такой алгоритм 1) 2) слова Наиболее употребительными являются Г. и. специального типа (так наз. инверсивные исчисления, см. [2]), у к-рых существование инвертирующего алгоритма обеспечивается надлежащим подбором их алфавитов и списков соотношений: алфавит инверсивного исчисления имеет четную длину, для каждой его буквы Роль Г. и. определяется тем, что они являются представлениями конечно определенных групп. Г. и. Упомянутый пример П. С. Новикова дает отрицательное решение и второй фундаментальной проблемы Дэна - проблемы распознавания пар слов, сопряженных в данном Г. и. Позднее П. С. Новиков [9] дал более простое и независимое от указанного примера отрицательное решение проблемы сопряженности. Большой интерес с алгебраич. точки зрения представляет изучение тех свойств Г. и., к-рые оказываются инвариантными относительно изоморфизмов Г. и.,- это свойства абстрактных конечно определенных групп. В 1955 С. И. Адян [10]-[12] получил весьма общий результат, аналогичный результату А. А. Маркова для ассоциативных исчислений, давший отрицательное решение практически всех известных в то время алго-ритмич. проблем, связанных с основными классификациями Г. и. В частности, им было получено отрицательное решение третьей проблемы Дена - проблемы изоморфии любой фиксированной конечно определенной группе. Впоследствии аналогичные результаты получил М. Рабин [13]. Неразрешимость упомянутых алгоритмич. проблем, касающихся Г. и., повлекла за собой отрицательное решение ряда алгоритмич. проблем топологии. проблема гомотопии путей. Опираясь на результаты С. И. Адяна, А. А. Марков получил в 1958 отрицательное решение проблемы гомеоморфин (см. [14]). Лит.:[1] Марков А. А., Теория алгорифмов, М., 1954; [2] его же, "Изв. АН СССР. Сер. матем.", 1963, т. 27, №4, с. 907-36; [3] Dehn M., "Math. Ann.", 1911, Bd 71, S. 116; [4] Magnus W., "J. reine und angew. Math.", 1931, Brt 163, № 2, S. 141-65; [5] Новиков П. С., "Докл. АН СССР", 1952, т. 85, с. 709-12; [6] его же, Об алгоритмической неразрешимости проблемы тождества слов в теории групп, М., 1955; [7] Воone W. W., "Indagat. math.", 1954, v. 16, p. 231, 492; 1955, v. 17, p. 252-56; 1957, v. 19, p. 22-7, 227-32; [8] Вrill on J. L., "Proc. London Math. Soc.", 3 ser., 1958, v. 8, № 32, p. 493-506; [9] Новиков П. С., "Изв. АН СССР. Сер. матем.", 1954, т. 18, № 6, с. 485-524; [10] Адян С. И., "Докл. АН СССР", 1955, т. 103, с. 533-35; [11] его же, там же, 1957, т. 117, № 1, с. 9-12; [12] его же, "Тр. Моск. матем. об-ва", 1957, т. 6, с. 231-98; [13] Rabin M. О., "Ann. Math.", 1958, v. 67, p. 172-94; [14] Марков А. А., "Докл. АН СССР", 1958, т. 121, №2, с. 218-20. Н. <М. <Нагорный. |
|
|
|

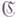 , что для всякого слова Рв алфавите Аисчисления
, что для всякого слова Рв алфавите Аисчисления  выполняются следующие условия:
выполняются следующие условия: определено и также является словом в А;
определено и также является словом в А; и
и  эквивалентны в
эквивалентны в  пустому слову (алгоритм здесь следует понимать в к.-л. точном смысле слова, напр, как нормальный алгорифм).
пустому слову (алгоритм здесь следует понимать в к.-л. точном смысле слова, напр, как нормальный алгорифм). явно указывается обратная ей буква
явно указывается обратная ей буква  , а в список соотношений включается полный набор так наз. тривиальных соотношений, т. е. соотношений, правые части к-рых суть пустые слова, а левые имеют вид
, а в список соотношений включается полный набор так наз. тривиальных соотношений, т. е. соотношений, правые части к-рых суть пустые слова, а левые имеют вид  .
. , как и всякое ассоциативное исчисление, стандартным образом (см. Ассоциативное исчисление).порождает конечно определенную ассоциативную систему
, как и всякое ассоциативное исчисление, стандартным образом (см. Ассоциативное исчисление).порождает конечно определенную ассоциативную систему  , к-рая вследствие наличия у
, к-рая вследствие наличия у  инвертирующего алгоритма оказывается группой. Алгоритмическая проблема распознавания эквивалентности слов в Г. и.
инвертирующего алгоритма оказывается группой. Алгоритмическая проблема распознавания эквивалентности слов в Г. и.  представляет собой формулированную в терминах Г. и. проблему тождества для конечно определенной группы
представляет собой формулированную в терминах Г. и. проблему тождества для конечно определенной группы  Это - первая из числа фундаментальных проблем разрешимости, сформулированных в 1911 М. Деном [3] для конечно определенных групп. Рядом авторов было найдено положительное решение этой проблемы для групп, определяемых частными типами Г. и. В частности, оно было получено для групп, определяемых инверсивными исчислениями с одним нетривиальным соотношением (см. [4]). В 1952 П. С. Новиков (см. [5], а также [6]) впервые построил пример конечно определенной группы с неразрешимой проблемой тождества, т. е. группы, порожденной таким Г. и., для к-рого невозможен никакой алгоритм в уточненном смысле слова (напр., Тьюринга машина или нормальный алгорифм), решающий проблему эквивалентности слов в этом Г. и. Этот пример дает отрицательное решение проблемы тождества для конкретной конечно определенной группы с учетом современного уточнения этой проблемы, даваемого теорией алгоритмов (см. Чёрча тезис). Впоследствии были приведены др. примеры таких Г. и. (см., напр., [7], [8]).
Это - первая из числа фундаментальных проблем разрешимости, сформулированных в 1911 М. Деном [3] для конечно определенных групп. Рядом авторов было найдено положительное решение этой проблемы для групп, определяемых частными типами Г. и. В частности, оно было получено для групп, определяемых инверсивными исчислениями с одним нетривиальным соотношением (см. [4]). В 1952 П. С. Новиков (см. [5], а также [6]) впервые построил пример конечно определенной группы с неразрешимой проблемой тождества, т. е. группы, порожденной таким Г. и., для к-рого невозможен никакой алгоритм в уточненном смысле слова (напр., Тьюринга машина или нормальный алгорифм), решающий проблему эквивалентности слов в этом Г. и. Этот пример дает отрицательное решение проблемы тождества для конкретной конечно определенной группы с учетом современного уточнения этой проблемы, даваемого теорией алгоритмов (см. Чёрча тезис). Впоследствии были приведены др. примеры таких Г. и. (см., напр., [7], [8]).