|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ГРУППОВАЯ СХЕМАЗначение ГРУППОВАЯ СХЕМА в математической энциклопедии: , схема групп,- обобщение понятия алгебраич. группы. Пусть
является контравариантным функтором из категории Примеры. 1) Алгебраич. группа над полем kесть приведенная Г. с. конечного типа над полем k. (Иногда алгебраич. группой наз. произвольную Г. с. конечного типа над полем.) 2) Функтор, сопоставляющий S-схеме Xаддитивную (соответственно мультипликативную) группу кольца сечений структурного пучка 3) Каждая абстрактная группа Г определяет Г. с. Для любой Г. с. Gсоответствующая приведенная схема Многие понятия и результаты теории алгебраич. групп имеют свои аналоги для Г. с. Напр., имеется аналог структурной теории Бореля - Шевалле для аффинных алгебраич. групп [5], развита когомологич. теория расширений Г. с. и однородных пространств над Г. с. (см. [2], [5]). С другой стороны, многие проблемы и результаты специфичны для теории Г. с. и связаны с наличием нильпотентных элементов в структурном пучке как базисной, так и самой Г. с. Так, изучаются ин-финитезимальные и формальные деформации Г. с. [4], вопросы подъема в нулевую характеристику, формальные пополнения Г. с. (см. Формальная группа). Г. с. естественным образом возникают при изучении алгебраич. групп над полем положительной характеристики (см. р-делимая группа). Понятие аффинной Г. с. над базисной аффинной схемой См. также Коммутативная групповая схема, Конечная групповая схема. Лит.:[1] Тейт Дж., Оорт Ф., "Математика", 1972, т. 16, № 1, с. 165-83; [2] Demazure M., Gabriel P., Groupes alg-cbriques, t. 1, P.-Amst., 1970; [3] Oort F., Commutative group schemes. В.-Hdlb.- N.Y., 1966; [4] его же, "Compositio math.", 1971, v. 23, p. 265-96; [5] Schemas en groupes, t. 1 - 3, В.- Hdlb.-N.Y., 1970. И. В. Долгачев. |
|
|
|

 - категория схем над базисной схемой
- категория схем над базисной схемой  ; групповой объект этой категории наз. групповой схемой над схемой
; групповой объект этой категории наз. групповой схемой над схемой  (а также групповой
(а также групповой  -схемой, или S-cхемой групп). Для Г. с. Gнад Sфунктор точек
-схемой, или S-cхемой групп). Для Г. с. Gнад Sфунктор точек 
 в категорию групп (Gr). Категория
в категорию групп (Gr). Категория  групповых схем над Sопределяется как полная подкатегория категории таких функторов, образованная представимыми функторами.
групповых схем над Sопределяется как полная подкатегория категории таких функторов, образованная представимыми функторами. представим. Соответствующая Г. с. над Sназ. аддитивной (соответственно мультипликативной) группой и обозначается
представим. Соответствующая Г. с. над Sназ. аддитивной (соответственно мультипликативной) группой и обозначается  (соответственно
(соответственно  ). Для любой
). Для любой  -схемы
-схемы 

 - прямую сумму семейства схем
- прямую сумму семейства схем  , каждая из к-рых изоморфна S. Соответствующий функтор сопоставляет S-схеме Xпрямую сумму
, каждая из к-рых изоморфна S. Соответствующий функтор сопоставляет S-схеме Xпрямую сумму  , где
, где  - множество связных компонент схемы X. Если G - Г. с. над S, то для любой точки
- множество связных компонент схемы X. Если G - Г. с. над S, то для любой точки  слой
слой  является Г. с. над полем вычетов k(s).этой точки. В частности, каждую Г. с. конечного типа над схемой Sможно рассматривать как семейство алгебраич. групп, параметризованное базой S. На Г. с. распространяется терминология теории схем; так, говорят о гладких, плоских, конечных, собственных Г. с.
является Г. с. над полем вычетов k(s).этой точки. В частности, каждую Г. с. конечного типа над схемой Sможно рассматривать как семейство алгебраич. групп, параметризованное базой S. На Г. с. распространяется терминология теории схем; так, говорят о гладких, плоских, конечных, собственных Г. с. также есть Г. с., для к-рой каноническое замкнутое вложение
также есть Г. с., для к-рой каноническое замкнутое вложение  есть морфизм Г. с. Каждая приведенная Г. с. локально конечного типа над полем является гладкой. Каждая Г. с. локально конечного типа над полем нулевой характеристики приведена (теорема Картье).
есть морфизм Г. с. Каждая приведенная Г. с. локально конечного типа над полем является гладкой. Каждая Г. с. локально конечного типа над полем нулевой характеристики приведена (теорема Картье). двойственно понятию коммутативной Хопфа алгебры, именно, если
двойственно понятию коммутативной Хопфа алгебры, именно, если 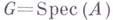 такая Г. с., то Аявляется коммутативной алгеброй Хопфа.
такая Г. с., то Аявляется коммутативной алгеброй Хопфа.