|
"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ГРИНА ФОРМУЛЫЗначение ГРИНА ФОРМУЛЫ в математической энциклопедии: - формулы интегрального исчисления функций многих переменных, связывающие значения га-кратного интеграла по области D n -мерного евклидова пространства криволинейный интеграл по контуру Г выражается через двойной интеграл по области Dот интенсивности (дивергенции)
распределенных в Dисточников и стоков. В этом смысле Г. ф. (1) подобна Остроградского формуле (см. также Стокса формула). Формула (1) иногда наз. именами К. Гаусса (С. Gauss) и Б. Римана (В. Riemann). Ни одно из употребляемых названий не является исторически верным: формула (1) встречалась еще в работах по анализу 18 в. - у Л. Эйлера (L. Euler) и др. Дж. Грину [1] принадлежат следующие Г. ф. потенциала теории -подготовительная Г. ф. и где D - область - оператор дифференцирования в направлении (ко) вектора N, а - оператор Лапласа. Формулы (2), (3) справедливы и в случае, когда Dесть область - оператор Лапласа с пнезависимыми переменными. Обобщения Г. ф. (2) и (3) для линейных дифференциальных операторов с частными производными с достаточно гладкими коэффициентами имеют вид: 1) если - (вещественно) сопряженные дифференциальные операторы второго порядка, где - оператор дифференцирования по направлению так наз. конормали 2) если где М - конормаль оператора L,a 3) если
- (вещественно) сопряженные дифференциальные операторы порядка
то Здесь граничный интеграл можно записать в виде билинейной суммы где Г. ф. играют важную роль в анализе и особенно в теории краевых задач для дифференциальных операторов (обыкновенных и с частными производными) второго и более высоких порядков. Для достаточно гладких в Для достаточно гладких в имеющей при Здесь число а Формулы (5) и (6) служат основой получения интегральных представлений решений основных краевых задач потенциала теории (см. Гармоническая функция, Грина функция, Пуассона формула). Напр., отсюда для гармонической в Dфункции и(х).получаем формулу, или интеграл Грина играющую важную роль в теории гармонических функций. Формулы, подобные формулам (5), (6), дающие интегральные представления решения задачи Коши или смешанной задачи, имеют место и для нормально гиперболич. оператора второго порядка. См. Кирхгофа формула, Римана метод, Римана функция. О Г. ф. в теории краевых задач см. также [4] -[9]. Лит.:[1] Green G., An essay on the application of mathematical analysis to the theories of electricity and magnetism. Nottingham, [1828]; [2] Максвелл Д., Избранные сочинения по теории электромагнитного поля, пер. с англ., М., 1954; [3] Смирнов В. И., Курс высшей математики, т. 2, 20 изд., М., 1966; [4] Курант Р., Уравнения с частными производными, пер. с англ., М., 1964; [5] Владимиров В. С., Уравнения математической физики, 2 изд., М., 1971; [6] Соболев С. Л., Уравнения математической физики, 4 изд., М., 1966; [7] Миранда К., Уравнения с частными производными эллиптического типа, пер. с итал., М., 1957; [8] Данфорд Н., Шварц Д ж. Т., Линейные операторы, пер. с англ., ч. 2, М., 1966; [9] Лионе Ж.-Л., Мадженес Э., Неоднородные граничные задачи и их приложения, пер. с франц., М., 1971. А. К. Гущин, Л. П. Купцов. |
|
|
|

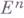 и
и  -кратного интеграла по кусочно гладкой границе
-кратного интеграла по кусочно гладкой границе  этой области. Г. ф. получаются интегрированием по частям интегралов от дивергенции векторного поля, непрерывного в
этой области. Г. ф. получаются интегрированием по частям интегралов от дивергенции векторного поля, непрерывного в  и непрерывно дифференцируемого в
и непрерывно дифференцируемого в  В простейшей Г. ф.
В простейшей Г. ф.
 . При этом область Dориентируется естественным образом, а на границе Г берется индуцированная ориентация, известная как обход против часовой стрелки. Формула (1) имеет простой гидродинамич. смысл: поток через границу области Г жидкости, текущей по плоскости со скоростью
. При этом область Dориентируется естественным образом, а на границе Г берется индуцированная ориентация, известная как обход против часовой стрелки. Формула (1) имеет простой гидродинамич. смысл: поток через границу области Г жидкости, текущей по плоскости со скоростью  , равен интегралу по области
, равен интегралу по области 


 ,
,  - элемент объема
- элемент объема  - элемент площади
- элемент площади  ,
,
 - единичная внешняя (ко)нормаль к Г,
- единичная внешняя (ко)нормаль к Г,

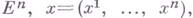
 - элемент объема
- элемент объема  - элемент ( п-1)-мерного объема Г, а
- элемент ( п-1)-мерного объема Г, а 

 , то
, то 
 - единичный (ко)вектор внешней нормали к Г,
- единичный (ко)вектор внешней нормали к Г,
 оператора L;
оператора L;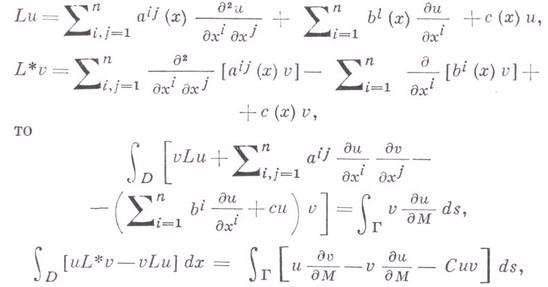


 - целочисленный мультииндекс длины
- целочисленный мультииндекс длины  ,
,



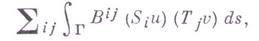
 - нек-рые линейные дифференциальные операторы порядков
- нек-рые линейные дифференциальные операторы порядков  .
. функций
функций  Г. ф. (2), (4) служат источником ряда соотношений, полезных для изучения свойств решения краевых задач, выяснения вида краевых задач, получения решения в явном виде и т. п. Напр., для гармонической в Dфункции
Г. ф. (2), (4) служат источником ряда соотношений, полезных для изучения свойств решения краевых задач, выяснения вида краевых задач, получения решения в явном виде и т. п. Напр., для гармонической в Dфункции  из (2) при
из (2) при  следует Гаусса теорема:
следует Гаусса теорема:
 функций и функции
функций и функции 

 такую же особенность, как и фундаментальное решение оператора Лапласа, верны следующие Г. ф.:
такую же особенность, как и фундаментальное решение оператора Лапласа, верны следующие Г. ф.:

 есть площадь
есть площадь  -мерной единичной сферы пространства
-мерной единичной сферы пространства  . При этом для
. При этом для  предполагается, что граница Г имеет непрерывную касательную плоскость в нек-рой окрестности у.
предполагается, что граница Г имеет непрерывную касательную плоскость в нек-рой окрестности у. (7)
(7)