"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ГРАФ СЛУЧАЙНЫЙ
Значение ГРАФ СЛУЧАЙНЫЙ в математической энциклопедии:
- вероятностная модель, предназначенная для изучения частотных характеристик различных параметров графов. Под Г. с. обычно понимается нек-рый класс графов  на к-ром задано распределение вероятностей. Произвольный конкретный граф Gиз
на к-ром задано распределение вероятностей. Произвольный конкретный граф Gиз  наз. реализацией Г. с. Всякая числовая характеристика графа (см. Графов числовые характеристики).может рассматриваться как случайная величина. Понятие Г. с. оказывается весьма полезным при моделировании сетей связи, подверженных нек-рым случайным изменениям, или логических сетей, элементы к-рых могут приходить в неисправные состояния; при рассмотрении картины фазовых превращений в статистич. физике; при изучении различных биологич. процессов; при решении задач минимизации булевых функций и др. В ряде случаев понятие Г. с. позволяет использовать аппарат теории вероятностей для получения асимптотич. решений перечислительных задач.
наз. реализацией Г. с. Всякая числовая характеристика графа (см. Графов числовые характеристики).может рассматриваться как случайная величина. Понятие Г. с. оказывается весьма полезным при моделировании сетей связи, подверженных нек-рым случайным изменениям, или логических сетей, элементы к-рых могут приходить в неисправные состояния; при рассмотрении картины фазовых превращений в статистич. физике; при изучении различных биологич. процессов; при решении задач минимизации булевых функций и др. В ряде случаев понятие Г. с. позволяет использовать аппарат теории вероятностей для получения асимптотич. решений перечислительных задач.
Одной из типичных является такая конструкция Г. с., при к-рой все реализации получаются в результате применения к заданному неслучайному графу G(чаще всего полному) нек-рой процедуры уничтожения его ребер; при этом обычно предполагается, что уничтожение различных ребер - события независимые и уничтожение ребра епроисходит с вероятностью д(е). Такую конструкцию Г. с. обозначают  Наибольший интерес представляет изучение различных числовых характеристик связности Г. с.
Наибольший интерес представляет изучение различных числовых характеристик связности Г. с. таких, как число компонент связности, диаметр, радиус, число связности и т. п., к-рые можно интерпретировать как характеристику надежности соответствующей сети связи или логической сети. В этом случае число
таких, как число компонент связности, диаметр, радиус, число связности и т. п., к-рые можно интерпретировать как характеристику надежности соответствующей сети связи или логической сети. В этом случае число 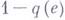 характеризует надежность связи е, а
характеризует надежность связи е, а  - вероятность выхода ее из строя.
- вероятность выхода ее из строя.
Если  - полный граф с пвершинами,
- полный граф с пвершинами,  ,
,  , то с вероятностью, стремящейся к 1 при
, то с вероятностью, стремящейся к 1 при  , Г. с.
, Г. с.  связен, имеет диаметр и радиус, равные 2, содержит гамильтонов цикл (см. Графа обход). Если
связен, имеет диаметр и радиус, равные 2, содержит гамильтонов цикл (см. Графа обход). Если  - функция числа вершин п, то вероятность связности Г. с.
- функция числа вершин п, то вероятность связности Г. с.  зависит от близости величины
зависит от близости величины  к
к 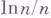 . Точнее, пусть
. Точнее, пусть

тогда  стремится к 1 при
стремится к 1 при  , если
, если 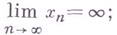 стремится к 0, если
стремится к 0, если  стремится к
стремится к  , если
, если  ( с - нек-рая константа). В последнем случае число ребер Г. с. асимптотически равно
( с - нек-рая константа). В последнем случае число ребер Г. с. асимптотически равно  .
.
Этот же Г. с.  может рассматриваться как граф, получаемый из неслучайного пустого n-вершинного графа путем случайного соединения его вершин ребрами так, что любая пара вершин соединяется независимо от остальных с вероятностью
может рассматриваться как граф, получаемый из неслучайного пустого n-вершинного графа путем случайного соединения его вершин ребрами так, что любая пара вершин соединяется независимо от остальных с вероятностью  . Этому способу образования графа
. Этому способу образования графа  можно придать динамику, если положить
можно придать динамику, если положить  и смотреть на tкак на время. При этом наблюдается следующая картина. В начальный момент времени t=0имеется пизолированных вершин. Затем с ростом tпоявляются нетривиальные компоненты связности, представляющие собой деревья или связные графы с одним циклом и малым числом вершин. Затем появляется одна "главная" компонента, содержащая число вершин, асимптотически равное п(при больших п). Дальнейший процесс характеризуется ростом главной компоненты и уменьшением числа малых компонент. Наконец, наступает момент, когда граф становится связным. Эту эволюцию Г. с. можно рассматривать как модель картины фазовых превращений, где роль жидкой фазы играет главная компонента, а роль разреженной фазы играют компоненты с малым числом вершин.
и смотреть на tкак на время. При этом наблюдается следующая картина. В начальный момент времени t=0имеется пизолированных вершин. Затем с ростом tпоявляются нетривиальные компоненты связности, представляющие собой деревья или связные графы с одним циклом и малым числом вершин. Затем появляется одна "главная" компонента, содержащая число вершин, асимптотически равное п(при больших п). Дальнейший процесс характеризуется ростом главной компоненты и уменьшением числа малых компонент. Наконец, наступает момент, когда граф становится связным. Эту эволюцию Г. с. можно рассматривать как модель картины фазовых превращений, где роль жидкой фазы играет главная компонента, а роль разреженной фазы играют компоненты с малым числом вершин.
Существует много других видов Г. с., напр. Г. с., связанные с деревьями (случайные деревья), с однозначными отображениями конечного множества в себя (случайные отображения), с подграфами единичного n-мерного куба (случайные булевы функции).
Лит.:[1] Мур Э. Ф., Шеннон К. Э., "Кибернетический сборник", 1960, в. 1, с. 109-48; [2] Степанов В. Е., в кн.: Вопросы кибернетики. Труды семинара по комбинаторной математике, М., 1973, с. 164-85; [3] Дискретная математика и математические вопросы кибернетики, т. 1, М., 1974; [4] Сапоженко А. А., "Проблемы кибернетики", 1975, в. 30, с. 227-61. А. А. Сапоженко,

 на к-ром задано распределение вероятностей. Произвольный конкретный граф Gиз
на к-ром задано распределение вероятностей. Произвольный конкретный граф Gиз  наз. реализацией Г. с. Всякая числовая характеристика графа (см. Графов числовые характеристики).может рассматриваться как случайная величина. Понятие Г. с. оказывается весьма полезным при моделировании сетей связи, подверженных нек-рым случайным изменениям, или логических сетей, элементы к-рых могут приходить в неисправные состояния; при рассмотрении картины фазовых превращений в статистич. физике; при изучении различных биологич. процессов; при решении задач минимизации булевых функций и др. В ряде случаев понятие Г. с. позволяет использовать аппарат теории вероятностей для получения асимптотич. решений перечислительных задач.
наз. реализацией Г. с. Всякая числовая характеристика графа (см. Графов числовые характеристики).может рассматриваться как случайная величина. Понятие Г. с. оказывается весьма полезным при моделировании сетей связи, подверженных нек-рым случайным изменениям, или логических сетей, элементы к-рых могут приходить в неисправные состояния; при рассмотрении картины фазовых превращений в статистич. физике; при изучении различных биологич. процессов; при решении задач минимизации булевых функций и др. В ряде случаев понятие Г. с. позволяет использовать аппарат теории вероятностей для получения асимптотич. решений перечислительных задач. Наибольший интерес представляет изучение различных числовых характеристик связности Г. с.
Наибольший интерес представляет изучение различных числовых характеристик связности Г. с. таких, как число компонент связности, диаметр, радиус, число связности и т. п., к-рые можно интерпретировать как характеристику надежности соответствующей сети связи или логической сети. В этом случае число
таких, как число компонент связности, диаметр, радиус, число связности и т. п., к-рые можно интерпретировать как характеристику надежности соответствующей сети связи или логической сети. В этом случае число 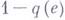 характеризует надежность связи е, а
характеризует надежность связи е, а  - вероятность выхода ее из строя.
- вероятность выхода ее из строя. - полный граф с пвершинами,
- полный граф с пвершинами,  ,
,  , то с вероятностью, стремящейся к 1 при
, то с вероятностью, стремящейся к 1 при  , Г. с.
, Г. с.  связен, имеет диаметр и радиус, равные 2, содержит гамильтонов цикл (см. Графа обход). Если
связен, имеет диаметр и радиус, равные 2, содержит гамильтонов цикл (см. Графа обход). Если  - функция числа вершин п, то вероятность связности Г. с.
- функция числа вершин п, то вероятность связности Г. с.  зависит от близости величины
зависит от близости величины  к
к 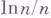 . Точнее, пусть
. Точнее, пусть 
 стремится к 1 при
стремится к 1 при  , если
, если 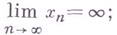 стремится к 0, если
стремится к 0, если  стремится к
стремится к  , если
, если  ( с - нек-рая константа). В последнем случае число ребер Г. с. асимптотически равно
( с - нек-рая константа). В последнем случае число ребер Г. с. асимптотически равно  .
. может рассматриваться как граф, получаемый из неслучайного пустого n-вершинного графа путем случайного соединения его вершин ребрами так, что любая пара вершин соединяется независимо от остальных с вероятностью
может рассматриваться как граф, получаемый из неслучайного пустого n-вершинного графа путем случайного соединения его вершин ребрами так, что любая пара вершин соединяется независимо от остальных с вероятностью  . Этому способу образования графа
. Этому способу образования графа  можно придать динамику, если положить
можно придать динамику, если положить  и смотреть на tкак на время. При этом наблюдается следующая картина. В начальный момент времени t=0имеется пизолированных вершин. Затем с ростом tпоявляются нетривиальные компоненты связности, представляющие собой деревья или связные графы с одним циклом и малым числом вершин. Затем появляется одна "главная" компонента, содержащая число вершин, асимптотически равное п(при больших п). Дальнейший процесс характеризуется ростом главной компоненты и уменьшением числа малых компонент. Наконец, наступает момент, когда граф становится связным. Эту эволюцию Г. с. можно рассматривать как модель картины фазовых превращений, где роль жидкой фазы играет главная компонента, а роль разреженной фазы играют компоненты с малым числом вершин.
и смотреть на tкак на время. При этом наблюдается следующая картина. В начальный момент времени t=0имеется пизолированных вершин. Затем с ростом tпоявляются нетривиальные компоненты связности, представляющие собой деревья или связные графы с одним циклом и малым числом вершин. Затем появляется одна "главная" компонента, содержащая число вершин, асимптотически равное п(при больших п). Дальнейший процесс характеризуется ростом главной компоненты и уменьшением числа малых компонент. Наконец, наступает момент, когда граф становится связным. Эту эволюцию Г. с. можно рассматривать как модель картины фазовых превращений, где роль жидкой фазы играет главная компонента, а роль разреженной фазы играют компоненты с малым числом вершин.