"
0
C
F
G
H
K
L
N
P
S
T
W
Z
А
Б
В
Г
Д
Е
Ж
З
И
Й
К
Л
М
Н
О
П
Р
С
Т
У
Ф
Х
Ц
Ч
Ш
Э
Ю
Я
ГРАФ ДВУДОЛЬНЫЙЗначение ГРАФ ДВУДОЛЬНЫЙ в математической энциклопедии:
бихроматический граф, - граф, множество вершин к-рого  можно разбить на два непересекающихся подмножества можно разбить на два непересекающихся подмножества  и , и ,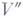 (т. <е. (т. <е. ) так, что каждое ребро соединяет нек-рую вершину из ) так, что каждое ребро соединяет нек-рую вершину из  с нек-рой вершиной из с нек-рой вершиной из  . Граф является Г. д. тогда и только тогда, когда все его простые циклы имеют четную длину. Под Г. д. часто понимают также граф, в к-ром заранее заданы подмножества вершин . Граф является Г. д. тогда и только тогда, когда все его простые циклы имеют четную длину. Под Г. д. часто понимают также граф, в к-ром заранее заданы подмножества вершин  и и  (доли). Г. д. удобны для представления бинарных отношений между элементами двух разных типов, напр.: взяв элементы данного множества и его подмножества, имеем отношение "вхождение элемента в подмножество"; для исполнителей и видов работ имеем отношение "данный исполнитель может выполнять данную работу" и т. д. (доли). Г. д. удобны для представления бинарных отношений между элементами двух разных типов, напр.: взяв элементы данного множества и его подмножества, имеем отношение "вхождение элемента в подмножество"; для исполнителей и видов работ имеем отношение "данный исполнитель может выполнять данную работу" и т. д.
Среди задач о Г. д. важное место занимает изучение паросочетаний, т. е. семейств попарно несмежных ребер. Такие задачи возникают, напр., в теории расписаний (разбиение ребер Г. д. на минимальное число непересекающихся паросочетаний), в задаче оназначениях(нахождениемаксимального паросочетания) и т. д. Мощность максимального паросочетания в Г. д. равна

где  - число вершин из - число вершин из  , смежных хотя бы с одной вершиной из , смежных хотя бы с одной вершиной из  . Полный Г. д.- это Г. д., в к-ром любые две вершины из различных подмножеств соединены ребром (напр., граф . Полный Г. д.- это Г. д., в к-ром любые две вершины из различных подмножеств соединены ребром (напр., граф  см. Граф плоский, рис. 1). Обобщением понятия "Г. д." является понятие "k-дольногографа", т. е. графа, в к-ром вершины разбиты на kподмножеств так, что каждое ребро соединяет вершины из разных подмножеств. Лит.:[1] Оре О., Теория графов, пер. с англ., М., 1968. см. Граф плоский, рис. 1). Обобщением понятия "Г. д." является понятие "k-дольногографа", т. е. графа, в к-ром вершины разбиты на kподмножеств так, что каждое ребро соединяет вершины из разных подмножеств. Лит.:[1] Оре О., Теория графов, пер. с англ., М., 1968.
В. Б. Алексеев.
|

 можно разбить на два непересекающихся подмножества
можно разбить на два непересекающихся подмножества  и ,
и ,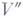 (т. <е.
(т. <е. ) так, что каждое ребро соединяет нек-рую вершину из
) так, что каждое ребро соединяет нек-рую вершину из  с нек-рой вершиной из
с нек-рой вершиной из  . Граф является Г. д. тогда и только тогда, когда все его простые циклы имеют четную длину. Под Г. д. часто понимают также граф, в к-ром заранее заданы подмножества вершин
. Граф является Г. д. тогда и только тогда, когда все его простые циклы имеют четную длину. Под Г. д. часто понимают также граф, в к-ром заранее заданы подмножества вершин  и
и  (доли). Г. д. удобны для представления бинарных отношений между элементами двух разных типов, напр.: взяв элементы данного множества и его подмножества, имеем отношение "вхождение элемента в подмножество"; для исполнителей и видов работ имеем отношение "данный исполнитель может выполнять данную работу" и т. д.
(доли). Г. д. удобны для представления бинарных отношений между элементами двух разных типов, напр.: взяв элементы данного множества и его подмножества, имеем отношение "вхождение элемента в подмножество"; для исполнителей и видов работ имеем отношение "данный исполнитель может выполнять данную работу" и т. д.
 - число вершин из
- число вершин из  , смежных хотя бы с одной вершиной из
, смежных хотя бы с одной вершиной из  . Полный Г. д.- это Г. д., в к-ром любые две вершины из различных подмножеств соединены ребром (напр., граф
. Полный Г. д.- это Г. д., в к-ром любые две вершины из различных подмножеств соединены ребром (напр., граф  см. Граф плоский, рис. 1). Обобщением понятия "Г. д." является понятие "k-дольногографа", т. е. графа, в к-ром вершины разбиты на kподмножеств так, что каждое ребро соединяет вершины из разных подмножеств. Лит.:[1] Оре О., Теория графов, пер. с англ., М., 1968.
см. Граф плоский, рис. 1). Обобщением понятия "Г. д." является понятие "k-дольногографа", т. е. графа, в к-ром вершины разбиты на kподмножеств так, что каждое ребро соединяет вершины из разных подмножеств. Лит.:[1] Оре О., Теория графов, пер. с англ., М., 1968.